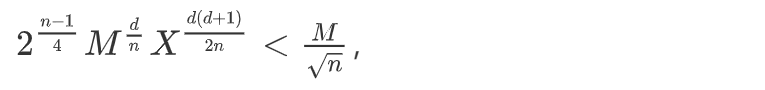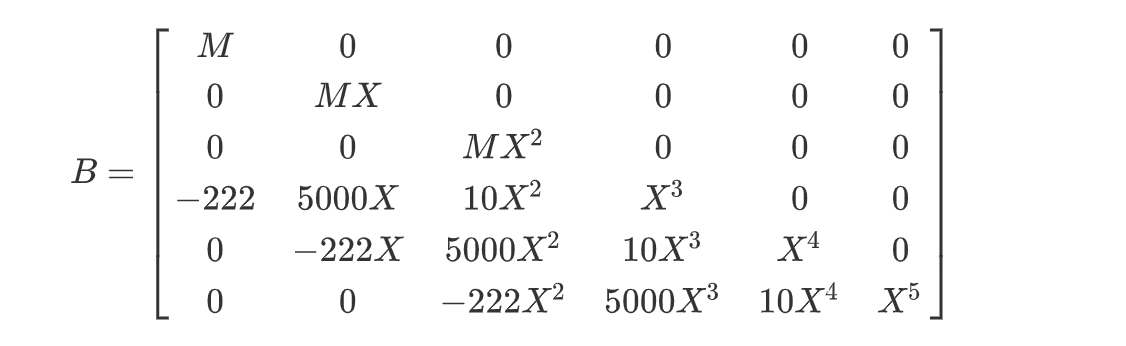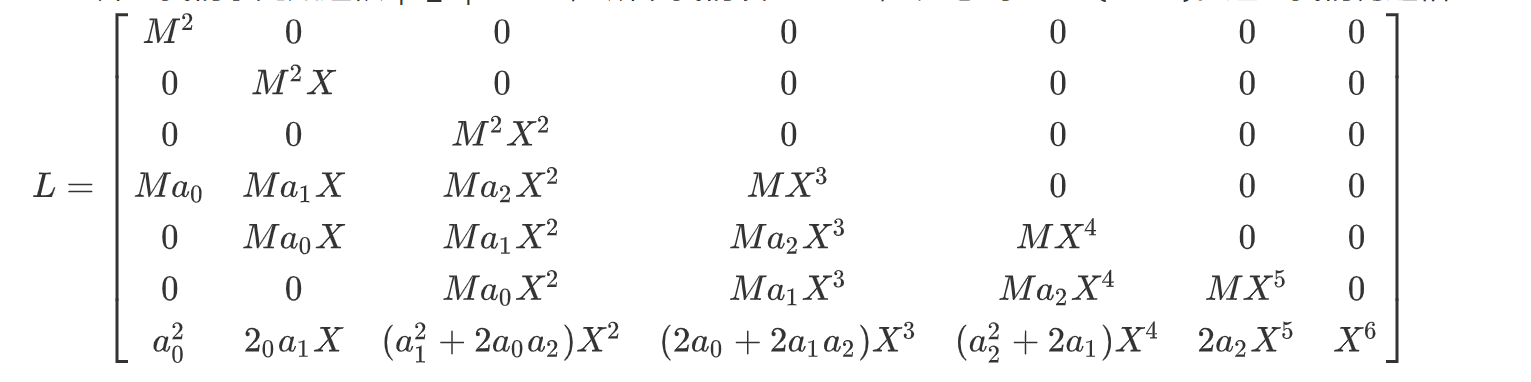The Full Coppersmith Method
这里回顾一下example 2,即使以M^{1/6}来计算边界也应该是4.6左右,那为什么我们设X = 10最终也可以得到正确的结果呢?其实审视一下整个过程,我们最终的目的只是为了获得一组系数,最后规约出来的行向量也都做了相应的”去除X“处理,所以这里对X的取值其实并不用特别严格。
其次,如果不取这个约来的边界M^{1/6}, 而是直接将d = 3带入
来计算这个x的边界,其实边界值应该是2.07左右。嗯?还是那个问题,那为啥我们可以得到正确结果呢?因为其实这个边界值也并不是很严格,在推导得出这个值的时候本身就用了很多次不等式,再者,我们利用的LLL中的那个性质,
我们取的是LLL算法规约出来的最坏的情况,而大多数情况得到的结果要比这值小许多。
回到这一章的主题,在上一章中我们对X的取值有不等式:
稍微还原一下就是
所以想要增加X就有两个思路,一个是往矩阵里多加几行向量来增加格的维度n,第二个就是增大M了。【这两个方法在公式层面看起来可能不那么直观,公式还需要再变形一下,并且应该也会有一个最优解】
针对第一种方案,我们称这种往格里插入的,增加了格的维度而不增加M的多项式为:“x-shift” polynomial,它们是x F(x), x^2 F(x), …, x^k * F(x),显然这些多项式在M下的解也为x0。
针对第二种方案,我们可以利用F(x)的幂来增加M,因为F(x0) ≡ 0 (mod M ),则有F(x0)^k ≡ 0 ( mod M^k )
我们继续拿上文中的example 2来举例,之前我们用到的格的维度n = 4,所以d = 3,带入那条不等式我们可以得到
M、X可得X ≈ 2.07,现在我们往格中添加两个多项式x F(x), x^2 F(x),得到
现在我们格的维度为6,并且行列式为M^3 * X^15,带入那条不等式可得
现在算出来X ≈ 3.11,可以看到通过添加“x-shift” polynomial,我们确实增大了X。
这里有一个现成的结论就是通过添加“x-shift” polynomial: x F(x), x^2 F(x), …, x^{d-1} * F(x),我们可以使得 X ≈ M^{1/(2d-1)},所以当d = 3,通过“x-shift” polynomial,我们将X ≈ M^{1/6 }提升为X ≈ M^{1/5}。那么如果在此基础上再增加了M呢?
Theorem 2 (Coppersmith)
设0< ε <min {0.18,1/d} ,F(x)为度为d的首一多项式,如果其在域M下有一个或多个根x = 0满足|x0|< M^{1/d-ε},那么我们就可以在与d,1/ε, log(M)相关的多项式时间内找到它,
proof
(同样,由于公式太多,加上平台无法显示latex公式,这里我就直接截图了)
example 3
设p=2^30 + 3,q=2^32 +15,M=pq
F(x)=a0+a1 x+a2 x^2+a3 * x^3=1942528644709637042 + 1234567890123456789x + 987654321987654321x^2 + x^3
并且我们事先知道根:|x0| ≤ 2^14, 所以我们设X = 2^14, 注意到X ≈ M^{1/4.4}。这里我们构造格
注意到,我们这里并没有像proof中的那样,加上所有的G(x),这里我们只添加量两条“x-shift” polynomial,额外添加了一条F(X)^2,第四行为M F(X)。理论上我们还可以针对F(X)^2再添加两条“x-shift” polynomial,但这里并没有这么做,是综合考虑了到x0的上界X,和LLL算法运行的时间复杂度。所以这里格的维度是7,行列式det(L)=M^9 X^21。
这里运行LLL算法,并将第一行的行向量的相应X值去除得到系数向量,可得G(x)=-369928294330603367352173305173409792 + 88565517701781911148679362207202x
-3439987357258441728608570659x^2 + 446358057645551896819258x^3
+4564259979987386926x^4 – 1728007960413053x^5 – 21177681998x^6
运算求根算法可得x0=16384
到这里,我们对于单元Coppersmith’s Method的原理学习就告一段落了。至于最初说的x0的取值上界可以达到M^{1/d}-ε},而为啥最后我们证明出来的是却是1/2 * M^{1/d-ε}。从Coppersmith 定理的证明过程来看,应该是与α的取值范围有关。【学艺不精,若有错误,还请大佬们轻锤】