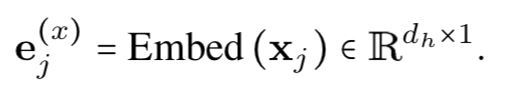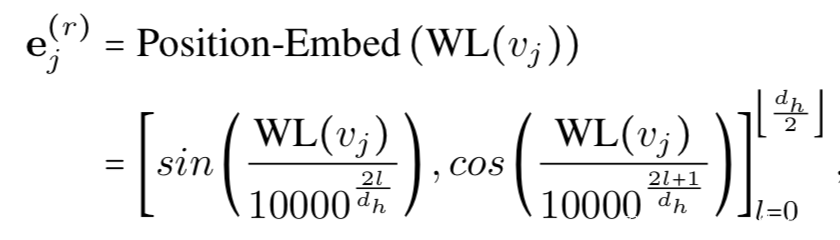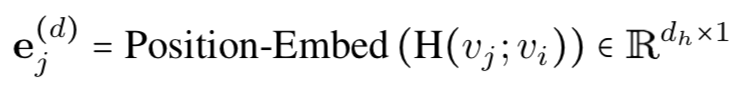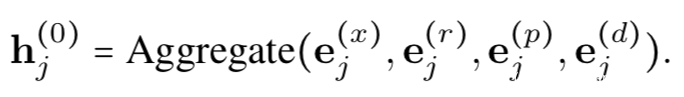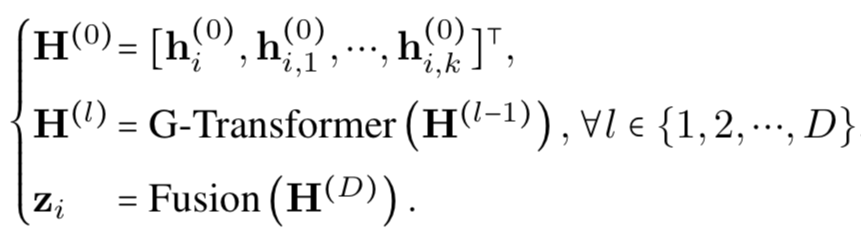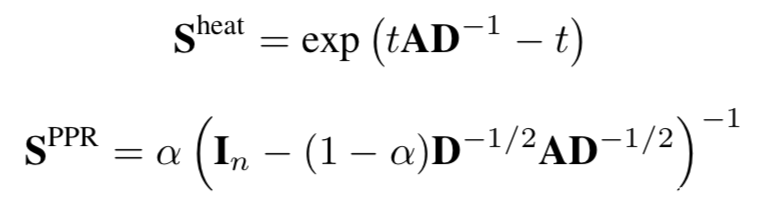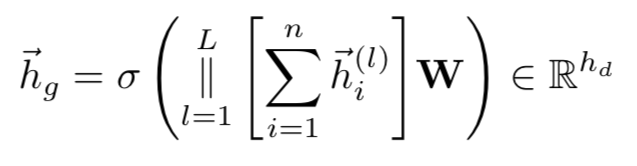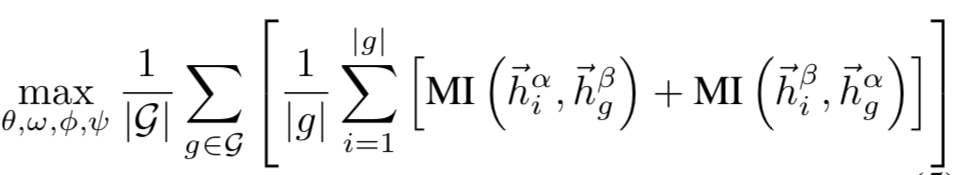摘要:
近年来,深度学习在视觉以及自然语言处理等领域取得了革命性的进步,但是诸如图像与自然语言之类的数据往往是高度结构与顺序化的。然而实际中大多数数据并无此特性,例如人际关系、社交网络、蛋白质分子结构等等,这些数据往往都具有一对多、多对一、非结构化等特性,无法使用矩阵完美表示,然而这些数据可以用图的形式进行精确表达。将深度学习的技术与思想应用于图数据结构之上催生了图神经网络。图神经网络可以捕获节点之间依赖关系,根据节点自身以及其周围邻域节点的信息建立状态的内部表示,以此获得比神经网络更为强大的表示能力。
通常,监督学习需要海量的带有标注的数据注释,在实际生活与工业界中,企业往往拥有大量数据,但这些数据往往只有极少数经过标注。这催生了自监督和无监督学习的兴起。对于图像和文本领域中的自监督学习在近几年获得了长足进步,但是由于图数据的特殊性与复杂性。如何将自监督与无监督学习应用于图神经网络中仍是当前学界与工业界面临的巨大挑战。
最近的一些研究发现很多自监督与无监督学习的技术思想也可适用于图类型的数据,我们在设计用于检测漏洞的图神经网络过程中也受到了很多来自CV、NLP领域自监督学习的启发来设计模型,我们今天将介绍一些其他研究者已经发表出来的相关的工作。
GRAPH-BERT
GRAPH-BERT是一种仅使用注意力机制的图神经网络。传统的图表示学习算法侧重于图的结构,即节点之间的连接。通过对目标节点与其邻域的连接来进行信息的聚合,此种方法可以有效的表示图的结构信息,但是此类图表示学习网络绝大多数都只能工作在浅层网络上,随着网络深度的加深,模型的性能会逐渐下降,并不再对训练数据产生响应。并且随着模型深度的加深,模型对节点的表示会变得过度平滑,难以对节点表示进行区分。
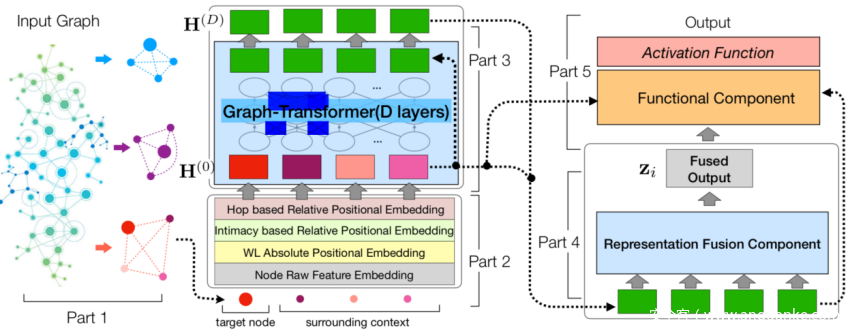
GRAPH-BERT不依赖于图中连接即可进行图表示,GRAPH-BERT总体分为五个模块:
1. 对无连接子图的批处理
2. 图的节点嵌入
3. 基于graph transformer的编码器
4. 图表示融合
5. 功能组件
GRAH-BERT算法流程图,在第五部分中,根据不同的目标,功能组件部分会生成不同的输出,这些输出及包括了目标节点,又包括了其周围的上下文节点
GRAPH-BERT不会一次处理整个图数据,而是会对输入图中进行无连接子图的随机批采样。这种方式可有效的使GRAPH-BERT得以在大型图上进行并行运算。之后便是对子图中的节点进行4种不同方式的嵌入:
1. 对节点的原始特征向量进行嵌入:
2. 为获取节点的全局信息,首先使用Weisfeiler-Lehman算法对图进行处理,该算法可以根据图中结构信息对节点进行聚合,具有相同结构的节点的标记亦相同。之后对节点的标记进行位置嵌入:
3. 基于Weisfeiler-Lehman的位置嵌入包函了节点的全局位置信息,但不同子结构中的相同节点在第2步中表示相同。由此引入对节点本身进行相对位置嵌入,以提取子图中的局部信息:
4. 为了平衡节点的全局信息嵌入与局部信息嵌入,加入基于跳跃的相对距离嵌入:
Graph transformer负责将所有的4个嵌入向量进行聚合,之后送入多层transformer编码器以得到新的表示:
可以使用两种任务对GRAPH-BERT进行无监督的预先训练:节点属性重构与图结构恢复。经过预训练的GRAPH-BERT可以将学习到的图表示直接输入到新的任务中,亦可以进行微调以适应下游任务。
Strategies for Pre-Training Graph Neural Networks
在许多机器学习参与的应用场景中,真实测试数据分布往往与训练数据的分布有所不同,并且有的任务往往只有少数带标注的训练数据。对于这类任务,首先在具有丰富且完善数据集的相关任务上对模型进行预训练,之后根据不同的下游任务进一步对模型进行微调的策略被证明是有效的。图神经网络的自监督学习大多数在节点级别或者整个图级别对模型进行预训练。但是由于图数据结构的特殊性,研究发现这两种级别的图自监督学习的发展空间有限,甚至有时反而会对下游任务起到负面作用。
对此研究者提出了一种新的预训练策略,该策略会同时在节点级别以及图级别对模型进行预训练,以便模型可以融合不同尺度的信息来进行决策。这种新的自监督学习策略可大大提高模型的泛化能力。
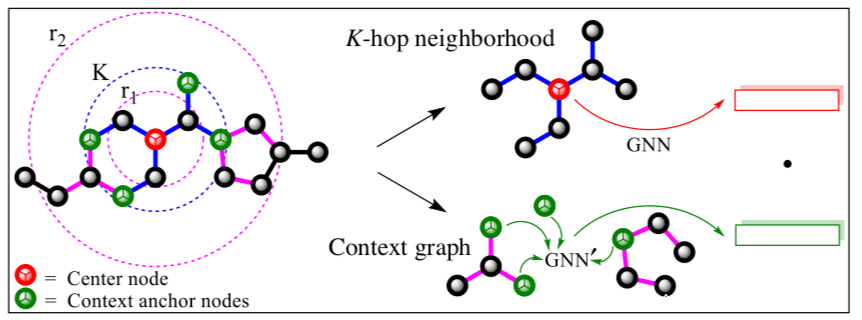
策略的第一步是先对模型进行节点级别的自监督训练,研究者们给出了两种节点级别的自监督训练方法:上下文预测和属性屏蔽。其中在上下文预测中:使用两个GNN模型,首先使用主GNN会对目标节点及其周围邻域进行聚合,将其编码成特征向量,其次会使用辅助GNN对目标节点的上下文进行聚合,并输出维度相同的特征向量。最后模型的输出为主GNN与辅助GNN编码的目标节点是否为同一节点的概率。在训练过程,可使用负采样算法,将负采样率设置为1,形成positive上下文与negative上下文的数据对。之后使用负对数似然作为损失函数进行训练。
上下文预测任务:主GNN负责表示中心节点及其k阶邻域内的节点,上下文定义为中心节点的r2阶与r1阶之间环形内的节点及其连接,r1,r2为超参数
节点级别训练的第二种方法是属性屏蔽,旨在使模型通过学习分布在图结构上的节点,边缘属性的规律性来捕获相关特征。首先mask掉图中节点或边缘属性,然后让GNN根据其相邻结构来对这些属性进行预测。
策略的第二步是在图级别对模型进行预训练,使模型得以学习特定领域的知识。此任务可通过对整个图中特定区域的属性进行预测或对图结构进行预测来实现。其中,前者可使用监督学习来实现,通过进行多任务监督式预训练可以使图级别的预训练模型面对下游任务时更加具有鲁棒性。
在分别对节点级别进行自监督训练和对图级别进行多人无监督训练之后,便可将得到的预训练模型用于相关的下游任务,例如,在图的分类任务中,通过在预训练模型之后添加线性分类器来预测图的标签,随后以端到端的方式对模型进行微调训练即可。
Contrastive Multi-View Representation Learning on Graphs
在计算机视觉中已被证明多视图表示学习可有效提高模型性能。受此启发,研究者将此引入图神经网络中,通过对同一图进行不同的结构视图变换,之后最大化变换后不同视图之间的互信息以进行训练。
对计算机视觉表示学习中的研究表明,通过对比视图可以使编码器学习更为丰富的表示。但相较于图片的数据增强手段(例如裁切、旋转、扭曲颜色等),首先需要在图类型数据上给出视图的定义。
同一个图的视图变换可从两个方面定义:
1. 在初始节点的特征空间上操作,例如掩膜或添加高斯噪声。
2. 对图的结构空间进行操作,例如添加或删除节点之间的连接,进行子图采样以及使用最短距离或扩散矩阵等方法来生成全局性视图。其中扩散矩阵可借助邻接矩阵进行生成。例如Personalized PageRank和Heat kernel便可看作两个扩散矩阵的实例,其分别定义为:
其中A为图的邻接矩阵,D为度矩阵,t为扩散时间, α为随机游走的跳转概率
在得到全局视图后,需要使用编码器来获取同一个图在不同视图下的表示,研究者用两个不同的图神经网络(此处使用GCN,也可使用不同的图神经网络)以及2个全连接网络(共享)和一个图池化层(共享)来建模编码器:同一个图的两个不同视图经过各自的GCN获得初级表示,之后分别经过第一个全连接层,图池化层,第二个全连接层进而获得两个视图的最终表示。其中图池化层(类似Readout)用于将GCN所学习到的节点级别表示聚合为图级别表示,其定义为:
将每层GCN得到的节点表示求和,之后对GCN所有层的求和结果进行拼接,在进行线性变换,最后经过激活函数得到结果
最后使用通过最大化一个视图节点级别的GCN表示与另一个视图上图级别表示之间的互信息(MI)对模型进行训练:
Hi为GCN对节点i的表示,hg为图g的表示,MI此处定义为两个向量的内积
算法流程:
总结
以上三篇论文都在一定程度上证明了将来自于有序数据结构上的自监督算法思想应用于图数据上的可能性以及有效性,结合图神经网络更加广泛的应用场景,自监督图神经网络的研究对学界和工业界都有着重大意义。因为受限于有标签数据的数量问题,我们在实践中设计漏洞检测神经网络的时候,从用于汇编语言表征的Instruction-BERT到节点表征、图表征,我们都大量使用了自监督学习。从效果上看,已经可以说,这些方法能够真正在工业界落地了,不再是漂浮在paper海洋中的空中楼阁。
总体来说,图神经网络还没有像卷积网络之于CV,Transformer之于NLP那样在工业界得到杀手级的应用,大规模知识图谱看起来是它能够大展身手的一个方向,但是离真正落地似乎还有距离。我们目前已经在将图神经网络应用于漏洞检测方面取得了一些进展,希望以后能够看到更多的相关研究在工业界落地。
引用文献:
[1] Zhang J, Zhang H, Sun L, et al. Graph-Bert: Only Attention is Needed for Learning Graph Representations[J]. arXiv preprint arXiv:2001.05140, 2020.
[2] Hu W, Liu B, Gomes J, et al. Strategies for Pre-training Graph Neural Networks[J]. arXiv preprint arXiv:1905.12265, 2019
[3] Hassani K, Khasahmadi A H. Contrastive Multi-View Representation Learning on Graphs[J]. arXiv preprint arXiv:2006.05582, 2020.