0x00前言
cryptopals是一套专注于密码学领域的攻防挑战题目。国内上海交大的GoSSIP小组曾分享set1和set2的writeup(https://loccs.sjtu.edu.cn/gossip/blog/2018/12/05/the-cryptopals-crypto-challenges-1/)不同于通过上课或者看书的方式学习密码学,这些题目来自于现在生活中一些软件系统和密码构造中的缺陷。本文将带来set3的writeup。
每一个题的wp基本是采用如下结构:题目解释、相关知识点讲解、代码实现及解释,运行测试。代码均采用python3实现,代码实现部分是参考国外大佬ricpacca的,结合自己的理解及成文需要进行部分修改。
第三套一共有八关。
这8个题目是关于分组密码学的,难度中等,包括针对CBC模式的典型攻击,针对RNG的cloning攻击等等。
接下来一一解决。
0x01
17题
这是针对分组密码学最著名的攻击手段
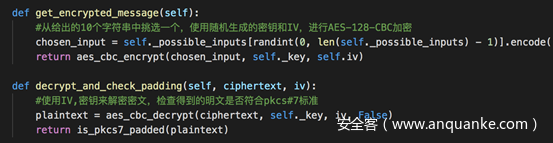
要求实现两个功能,一个功能从给出的10个字符串中随机选择一个,随机生成AES密钥,并进行填充,使用CBC模式进行加密。在需要时可以提供密文和IV
第二个功能则是解密密文,检查明文的填充是否有效,并以此返回true或者false
我们的目标是能够解密密文,这里解密依靠的是侧信道泄露,泄露的信息是判断解密后的明文的填充是否有效。
关于Padding Oracle Attack的介绍文章实在太多了,国内打CTF几年前就玩烂了,为了保持本系列的完整性,这里还是稍微展开介绍。如果有不清楚的地方,可以参考这篇文章,国内外很多文章都是参考它的:https://blog.gdssecurity.com/labs/2010/9/14/automated-padding-oracle-attacks-with-padbuster.html
关于这种攻击手段,有两块前置知识。一块是关于分组密码的填充,填充标准常用有的pkcs#5,pkcs#7,这在之前的文章中我们已经介绍过了。要注意的一点就是,在本次的攻击手段中就是通过判断得到的明文的填充是否符合标准,从而判断其是否有可能为正确的明文。
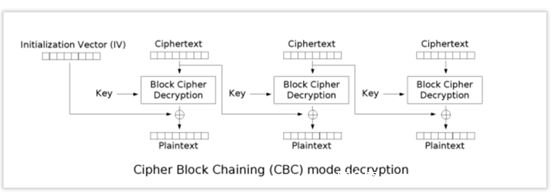
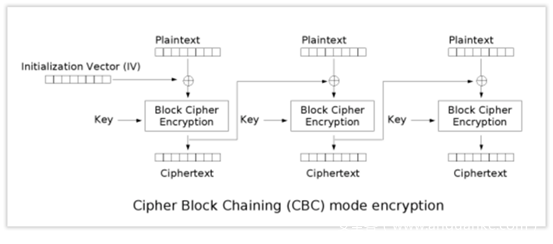
另一块就是CBC的加解密模式,我们之前也提过,不过这次的关注点不同。这里再次给出下图
这里注意到,以解密过程为例。
密文cipher不是解密后立刻得到明文的。
而是密文首先进行一系列处理,如图中的Block Cipher Decryption,我们将处理后的值称为intermediary value中间值,然后中间值与我们输入的iv进行异或操作,得到的即为明文。在解密下一分组时,第一个分组的密文则作为下一分组解密时的IV来使用,在第二个分组处理得到中间值后,与其异或得到第二个分组的明文,以此类推。
接下来我们举个例子。
假设已经知道中间值:0x39 0x73 0x23 0x22 0x07 0x6a 0x26 0x3d
原始的IV:0x6d 0x36 0x70 0x76 0x03 0x6e 0x22 0x39
两者异或后就可以得到明文:T E S T 0x04 0x04 0x04 0x04
但对于攻击者而言,攻击者只有正确的IV,但不知道中间值和正确解密得到的明文的。攻击者要做的就是,对IV进行暴力测试,与未知的中间值异或后,得到明文,如果明文的是按照标准填充的,则说明这一轮测试的Iv是有效的。
攻击者接下来会暴力测试IV:
从最后一位开始
第一轮的IV:0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00
与中间值异或得到明文
0x39 0x73 0x23 0x22 0x07 0x6a 0x26 0x3d
可是最后一位Padding的字节是0x3d,明显说明这是不合法的padding,继续推理,可知这一轮的IV是不合法的,于是继续测试,直到某一轮:
IV:0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x3c
与中间值异或得到明文:
0x39 0x73 0x23 0x22 0x07 0x6a 0x26 0x01
程序校验最后一位,发现是0x01,即可通过校验.
有公式:
Middle[8]^暴力测试的iv[8] = 0x01
所以middle[8]=暴力测试的iv[8] ^0x01
又因为Middle[8]^原始的iv[8] = 真正的plain[8]
所以真正的plain[8]=暴力测试的iv[8] ^0x01^原始的iv[8]
在我们的例子中,真正的plain[8]=0x01^0x3c^0x39=0x04(和我们正常解密得到的明文分组第8字节相符))
还可以得到middle[8]=原始的iv[8] ^真正的plain[8]=0x39^0x04=0x3d,这个值在下一轮会用到
接下来我们继续暴力测试IV,以期得到plain[7]
此时暴力测试iv时,需要注意,我们这次希望解密得到的明文末尾两字节是0x02
先看第8个字节
由于:iv[8]^middle[8]=0x02
所以iv[8]=middle[8]^0x02=0x3d^0x02=0x3f
然后固定iv[8],去暴力测试Iv[7],直到得到的明文分组的最后两字节是0x02 0x02即可
暴力测试到这时:
Iv:0x00 0x00 0x00 0x00 0x00 0x00 0x24 0x3f
Middle:
0x39 0x73 0x23 0x22 0x07 0x6a 0x26 0x3d
明文:0x39 0x73 0x23 0x22 0x07 0x6a 0x02 0x02
于是可以得到plain[7]=暴力测试的iv[7] ^0x02^原始的iv[7]=0x02^0x22^0x24=0x04(和我们正常解密得到的明文分组第7字节相符)
依次类推,即可解得明文
有了思路,代码就不难写了
先是按照题目要求,定义两个函数,分别用于加密和解密以及校验padding是否合法,这些功能在以前的题目题目中代码实现过,可以直接饮用
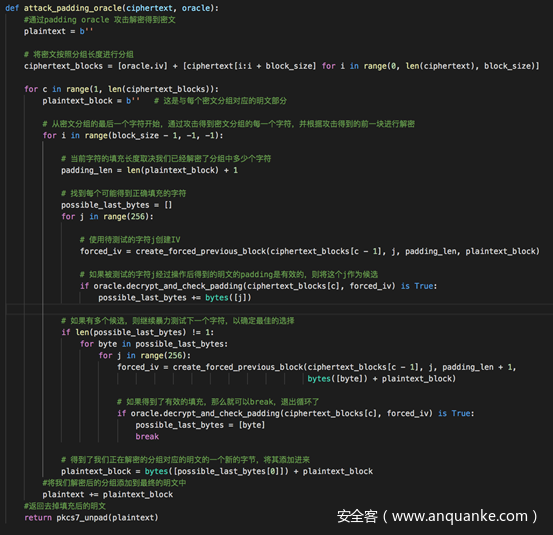
暴力测试IV,使得得到的IV能够有效解密密文,得到的明文符合填充标准
通过上面函数生成的IV,不断循环测试,一个个分组分别解密,得到明文
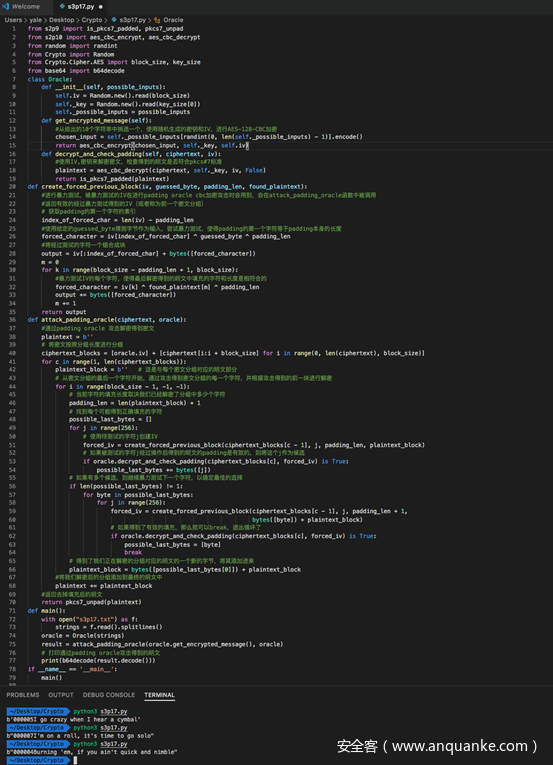
完整代码及测试结果如下
打印的结果是随机选择的密文解密后的明文
0x02
18题
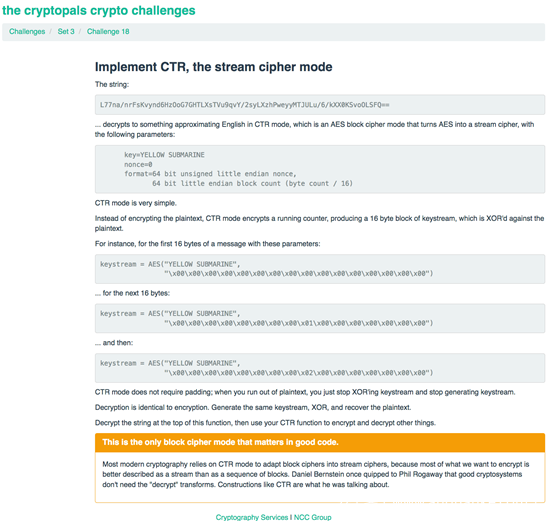
要求我们实现CTR模式。并针对给出的例子进行测试。
CTR模式是常见分组密码工作模式中的一种,其全称是CounTeR模式(计数器模式)。CTR模式是一种将逐次累加的计数器进行加密来生成密钥流的流密码
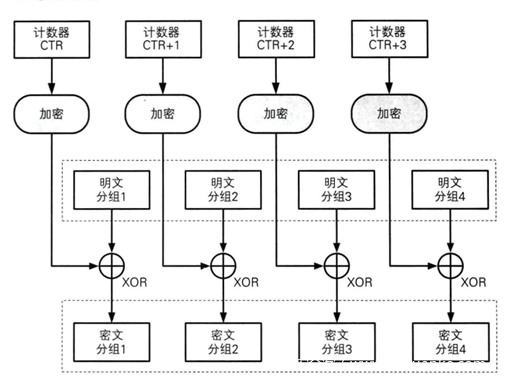
CTR模式中,每个分组对应一个逐次累加的计数器,并通过对计数器进行加密来生成密钥流。也就是说,最终的密文分组是通过将计数器加密得到的比特序列,与明文分组进行xor而得到的。
加密图示如下
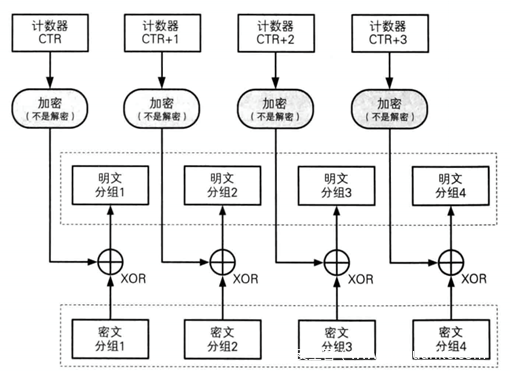
解密图示如下
从解密图示中我们可以看到,解密时只需要生成相同的密钥流,再异或就可以得到明文了。所以我们在写代码时,写一个函数就可以了
这里需要注意计数器的生成方法
每次加密时都会生成一个不同的值(nonce)来作为计数器的初始值
以分组长度为16字节为例,计数器的初值可能为:
前8个字节为nonce,这个值每次加密时都不同。后8字节为分组序号,这个部分会逐次累加。加密过程中,计数器的值可能会如下变化
这样就可以保证计数器的值每次都是不同的,因为对其加密得到的密钥流也是不同的。我们就是用分组密码来模拟生成的比特序列。
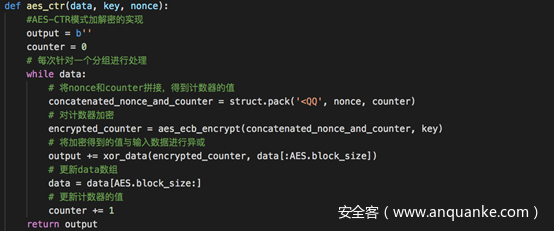
代码实现很简单,关键的函数就一个,用于实现AES-CTR模式加解密
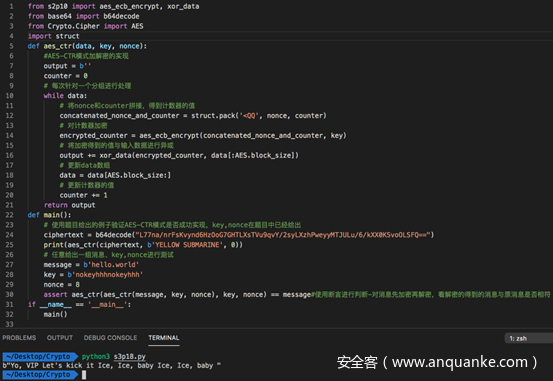
完整代码及测试如下
在main中首先是对给出的密文进行解密。然后又任意给了一个例子,对其加密、解密进行测试。
从结果可以看到,成功实现了AES-CTR模式。
0x03
第19题
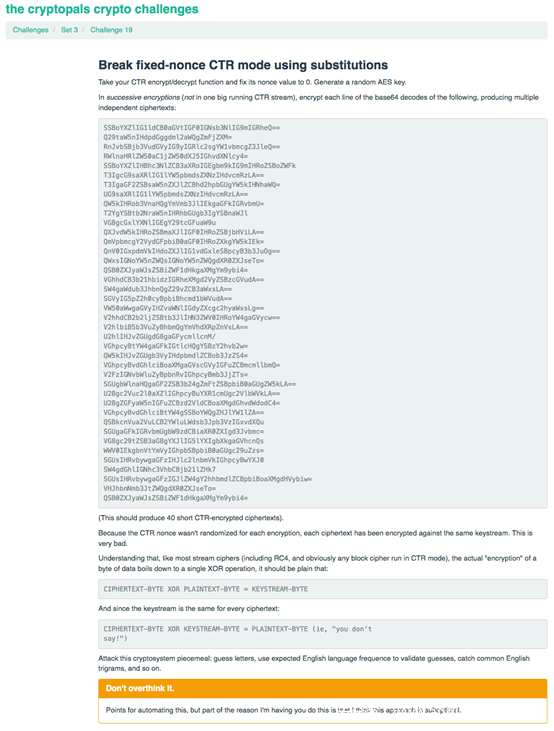
题目要求我们先对给出的40行经过base64编码的明文进行AES-CTR加密。这是为了模拟在某些情况下,在对大量的密文进行加密时,nonce并不会每次都是随机变化的,可能在加密时使用的是相同的密钥流。
而攻击者在解密时,会假设大量的密文都是使用相同的密钥流与明文异或得到。这样,我们就可以将可能的密钥流的每个字节分别通过循环,与密文异或,通过计算得到的明文,根据其分值,得到最可能的密钥流。然后在根据得到的密钥流进行解密即可。
这种方法可以得到大部分正确的明文,不过还是有些明文会解密错误。原因后续在分析代码时再解释。
总之通过这道题目我们可以学会:在大量的密文使用相同的nonce加密时,如何对其攻击得到明文。
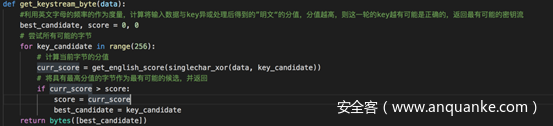
写一个通过计算明文中的字母频率累加值来得到密钥流的函数
以及攻击的函数
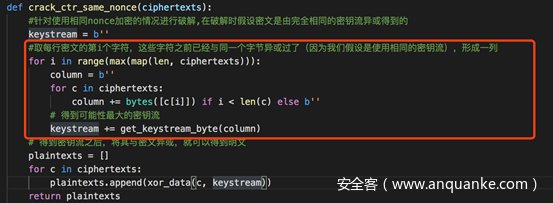
红色框起来的部分,就是我之前提到为什么会有少部分明文解密失败的原因。
这里在调用获取密钥流的函数get_keystream_byte时,传入的column作为data参数,而column是从每行密文中综合得到的,而每行密文长度不一,所以在计算时column作为data参数并不十分精确。
这一点我们待会儿测试时可以验证。
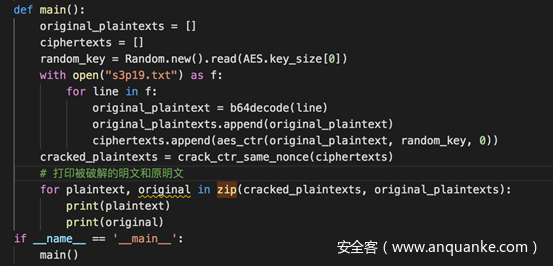
在main中打印使用这种攻击手段破解的明文和原明文
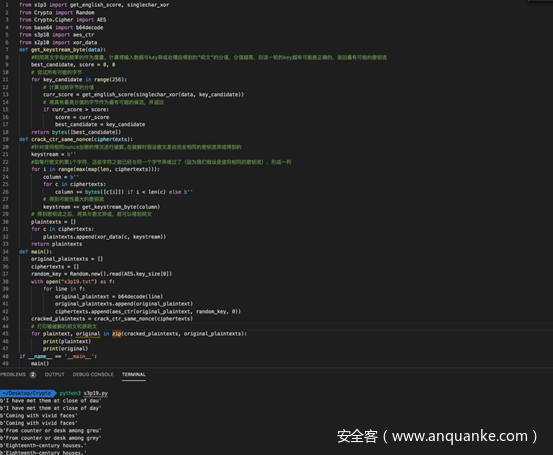
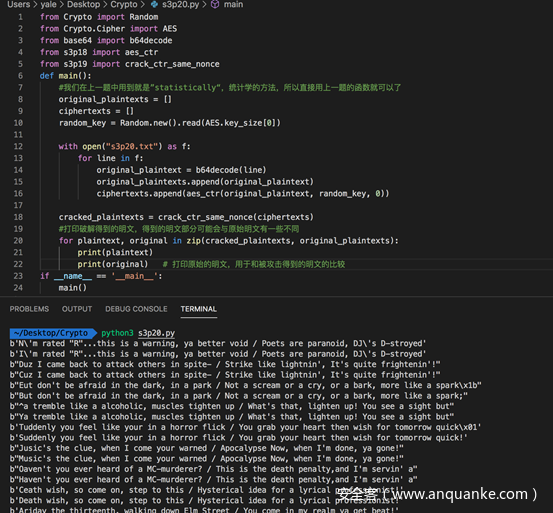
全部代码及测试如下
上一行是攻击得到的明文,下一行是原始明文,如我们分析的一样,两者是有些差别的,不过差别不大,基本可以辨认。
0x04
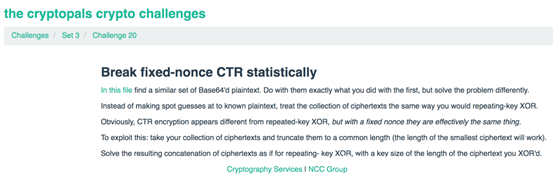
第20题
题目给出一个文件,文件里还是base64编码过的明文,要求我们对其进行AES-CTR加密,之后对其模拟攻击,进行解密。这里所谓的”statistically”,指的是利用统计学的方法,其实我们在上一题中就是用这种办法攻击的。”统计学的方法“体现在两个方面,一方面是在取密文传入get_keystream_byte时,所有的密文都参与了;一方面是在get_keystream_byte本身而言,计算每次得到的明文的数值就是用的统计学的方法,根据频率将明文的每个字母加入运算得到最终的数值。
所以本题的代码没有特别的地方,我们直接看全部代码及测试结果:
0x05
第21题
题目要求我们实现MT19937,它是Mersenne Twister的一种变体,可以产生32位整数序列
梅森旋转算法(Mersenne twister)是一个伪随机数发生算法。由松本真和西村拓士在1997年开发,基于有限二进制字段上的矩阵线性递归F。可以快速产生高质量的伪随机数,修正了古典随机数发生算法的很多缺陷。
Mersenne Twister这个名字来自周期长度取自梅森素数的这样一个事实。这个算法通常使用两个相近的变体,不同之处在于使用了不同的梅森素数。一个更新的和更常用的是MT19937, 32位字长。还有一个变种是64位版的MT19937-64。对于一个k位的长度,Mersenne Twister会在 [0,2^{k}-1]的区间之间生成离散型均匀分布的随机数。
MT19937的优点包括:
1.周期非常长,达到2^19937−1。尽管如此长的周期并不必然意味着高质量的伪随机数,但短周期(比如许多旧版本软件包提供的2^32)确实会带来许多问题。
2. 在1 ≤ k ≤ 623的维度之间都可以均等分布。
3.除了在统计学意义上的不正确的随机数生成器以外,在所有伪随机数生成器法中是最快的(就算法提出时而言)
后面几题都是与随机数相关的题目,所以这里关于随机数再说明一下:
随机数在许多领域中都有着大量应用,例如密码学,游戏,数学统计。随机数主要分两类,分别是确定性随机数和非确定性随机数。非确定性随机数也可称为真随机数(True Random Number Generator, TRNG),主要来源于不可预测的物理或者化学熵源,例如电路噪声。真随机数发生器产生的随机数质量十分高,是最理想的随机数来源,但是由于产生的速度太慢,无法满足目前的信息的传输速度,因此目前确定性随机数依然被广泛使用。确定性随机数发生器也称作伪随机数发生器(Pseudorandom Number Generator,PRNG),它一般是一个随机数生成算法,由于算法是固定的,因此生成的随机数存在许多诸如可预测,质量不高的缺点。
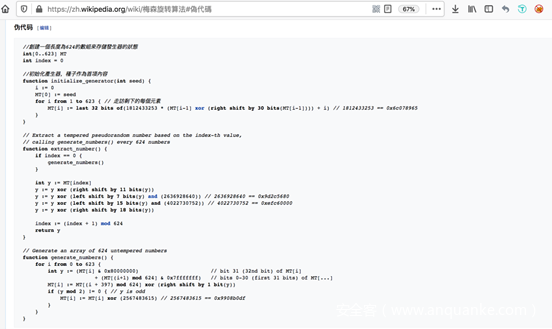
回到题目,题目提示我们可以在维基百科上找到伪代码,如下图所示
另外,题目告诉我们使用python,ruby,php等语言,已经内置实现了MT19937,而题目要求我们手动实现。
在实现时会用到一些数据,我们先给出
梅森旋转算法实际使用的是旋转的广义反馈移位寄存器(Twisted Generalized Feedback Shift Register,GFSR),它主要分初始化,旋转生成随机数以及Xorshift后期处理三个步骤。由于MT19937的梅森算法中生成的随机数为32位,因此算法需要624个32位长的状态。在初始化阶段,即下图的init,工作是将我们获得的随机种子经处理填充到所有的624个状态中
函数将输入的随机种子赋值给第0个状态,剩余的623个状态则用前一状态值的一系列操作进行赋值更新。当执行完这一算法后,全部的624个状态已经填充完毕,之后梅森算法便可以不断地生成伪随机数。
接着是旋转生成随机数
MT19937标准中定义A的值为0x9908B0DF。这部分是进行旋转操作。每生成624个伪随机数后,将执行一次上面的函数,重新更新624个状态,为生成下一批624个伪随机数做准备。
之后是第三步后期处理,每个状态都需要经过Xorshift操作以后才能成为最终输出的伪随机数,由于其中几乎都是移位,因此对CPU来说处理起来非常快。
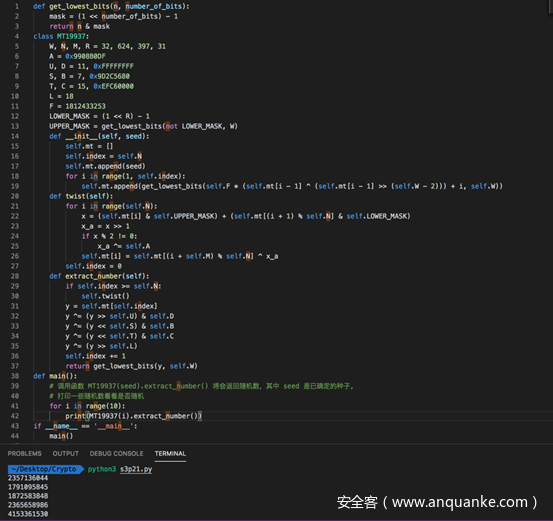
完整的代码及测试如下
这样我们就手动实现了MT19937
这里参考了中科院信工所发表的《梅森旋转算法安全性分析及改进》,想进一步了解的同学可以看看这篇论文
0x06
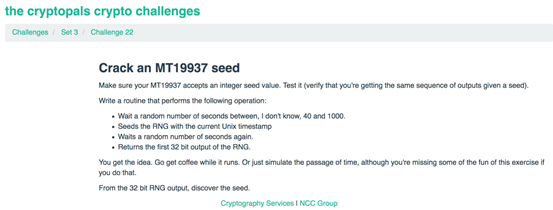
第22题
要求我们实现以下操作:
在40到1000之间随机等待几秒钟
使用当前的Unix时间戳作为种子
再次等待随机秒数。
返回种子、随机数
题目要求我们能够从输出中破解得到种子
题目还提示我们可以模拟时间,从而避免真的要等待一段随机的时长
第一个函数要实现题目要求我们做的操作
我们就是要逆向破解得到这个函数返回的随机数。随机数在rng.extract_number()
将该值作为参数传入破解种子的函数
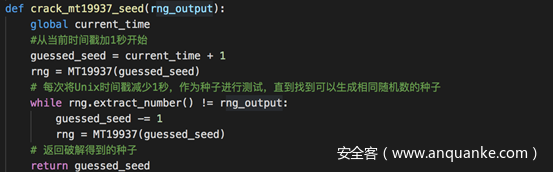
这里的破解其实很简单,就是不断地测试、改变可能作为种子的时间戳,判断其生成的随机数是否等于第一次生成的随机数,如果是,则说明找到了正确的种子,返回即可
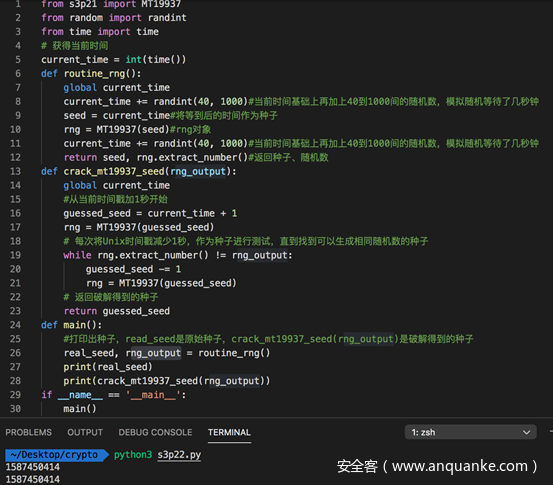
完整的代码及测试如下
第一行是原种子,第二行是我们暴力破解得到的种子。在实际运行时,会发现过了一会儿才会打印出第二行的结果,这是因为程序正在跑crack_mt19937_seed
0x07
第23题
有三个关键的点需要把握住:
- 要知道MT 19337完整的内部状态由624个32位整数组成,如果可以克隆这些整数,则可以预测RNG之后生成的数
- 内部状态中的每个整数都按顺序直接与RNG的输出一一对应。
- 内部状态中的每个整数与输出的随机数的对应关系是可逆的关系。换句话说,给定了RNG的输出,我们可以逆向得到与之相关联的内部状态中的整数
综合以上三点,如果我们逆向得到了组成状态的624个整数,只需将这个状态复制到自己的MT 19937 RNG中,就可以得到原RNG的一个有效的克隆,可以预测之后的“随机数”
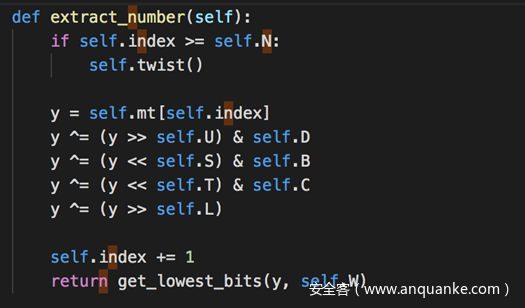
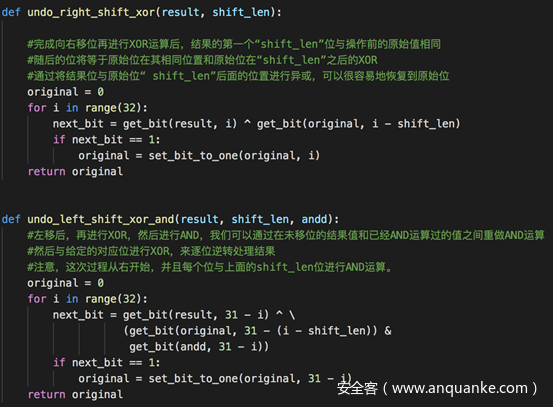
RNG的输出是容易拿到的,关键是怎么得到内部状态。题目提示我们生成随机数的temper函数是可逆的(就是我们在前面代码中写的extract_number函数,为了与题目相统一,接下来一律称为temper),我们写一个untemper函数,接收MT19937输出并将其转换回MT19937状态数组的相应元素即可。要逆向temper所做的事情,我们需要按照相反的顺序实现temper中的每个操作的逆操作。temper中有两种操作,每种操作应用了两次,一个是对右移值(right-shifted)的XOR,另一个是对左移(left-shifted)值的XOR,并与一个幻数进行与运算,我们只需要逆着实现就可以了
先写两个逆操作的函数
然后在untemper中调用即可
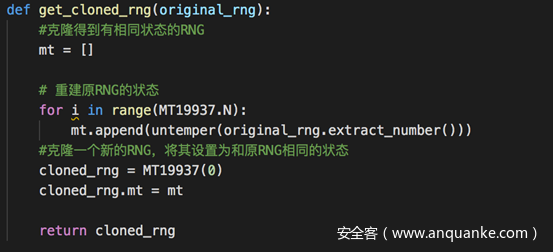
接下来就是克隆一个新的RNG
新的RNG克隆了与原RNG相同的状态
然后在main中分别使用两个RNG生成随机数,便于比较
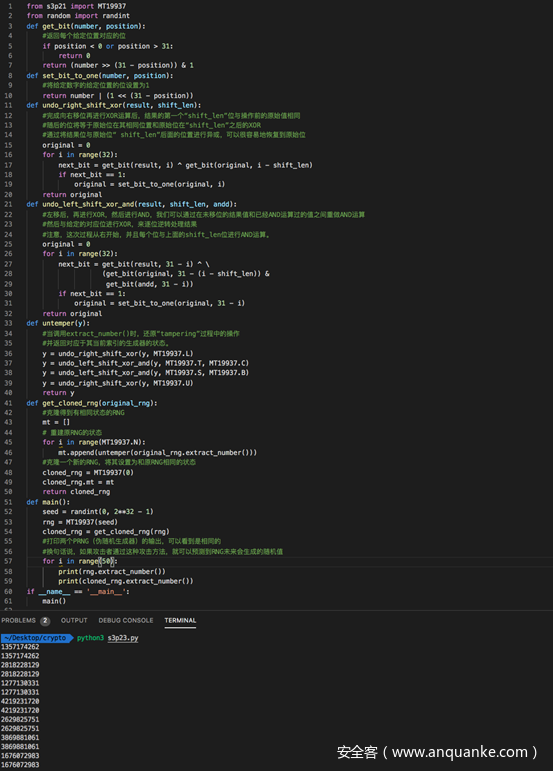
完整代码及测试结果如下
可以看到两个RNG的输出是相同的,或者换句话说,攻击者通过本题介绍的攻击方法,可以克隆得到一个新的RNG用于预测原RNG生成的随机数
0x08
第24题
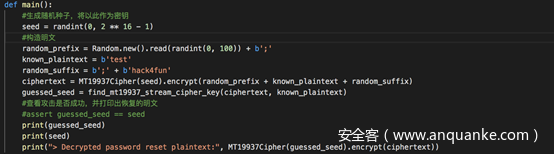
题目要求实现:使用16位的种子传入MT 19937 RNG,生成的随机数作为密钥流。以该密钥流对明文加密(明文可以任意,可以加前缀、后缀)。然后暴力测试可能的密钥(16位的种子),对密文解密
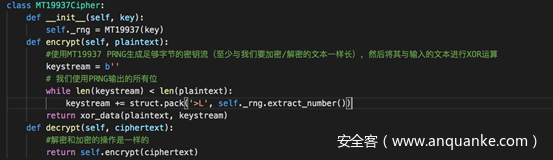
题目没有指定加解密的算法,为了简单起见,我们指定加密算法为将RNG生成的密钥流与明文异或,这样解密和加密就是同样的操作了
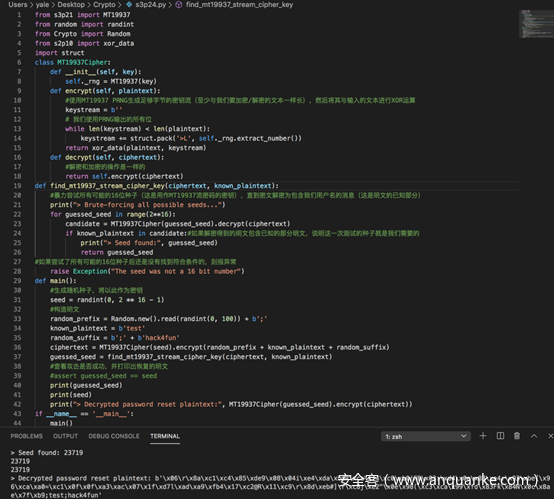
暴力测试可能的密钥的函数如下
在main中构造任意明文,加密得到密文,然后调用find_mt19937_stream_cipher_key,经过暴力测试得到密钥,最后用得到的密钥对密文进行解密
三个print语句分别是用于打印暴力测试得到的密钥,和原密钥,以及使用暴力破解得到的密钥解密出的明文。
完整代码及测试结果如下
可以看到,暴力破解得到的密钥和原密钥是相同的,并且密文也被成功解密了。
参考:
1.https://cryptopals.com/sets/3
2.https://github.com/ricpacca/cryptopals
3.布鲁斯《应用密码学》(研究密码学必看,强烈推荐)