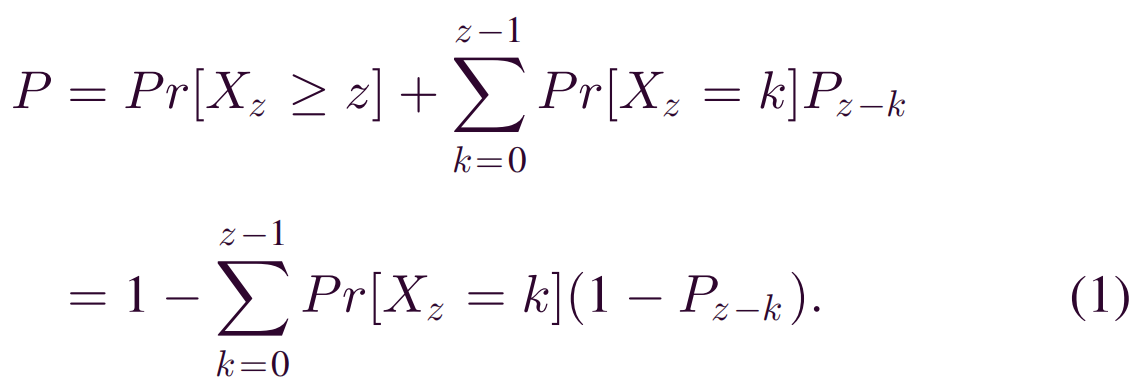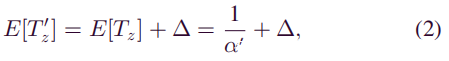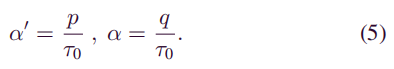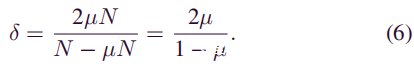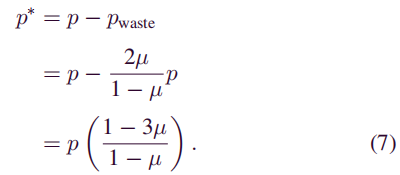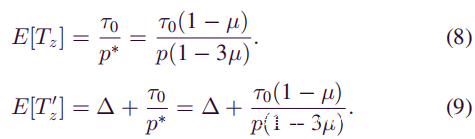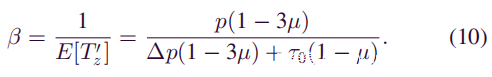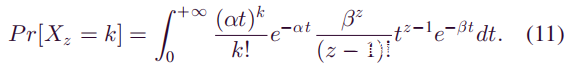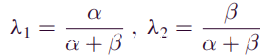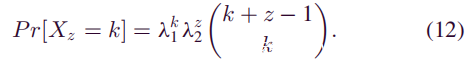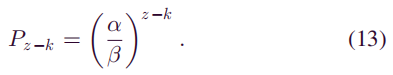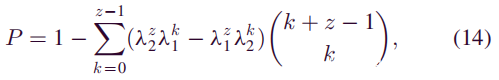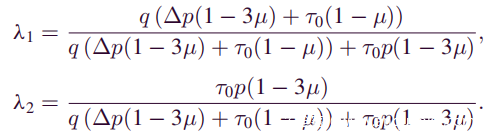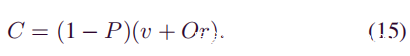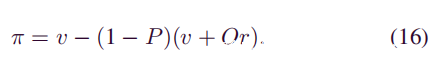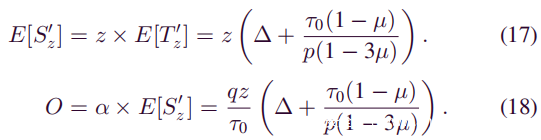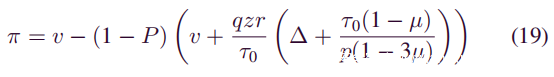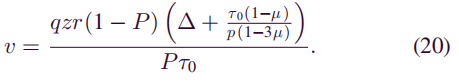双花攻击者可以通过组合Sybil攻击来阻止块传播,并增加赢得挖矿竞争的概率,从而成功地发起了双花攻击。本文计算了这种新攻击的成功可能性,并从经济学的角度分析这种攻击模型。将介绍攻击者在各种情况下的收支平衡点,并演示攻击的效果。
0x01 Introduction
在上一篇文章中介绍了一种新的组合攻击模型。通过引入Sybil攻击来影响比特币节点之间的通信协议(即gossip协议)来增加块传播延迟。研究了在Sybil攻击下成功进行双花攻击的可能性。研究取得了很好的结果,即只有比特币网络中32%的计算能力份额的攻击者可以成功地双花。
本文对该攻击模型进行了经济评估,以找到攻击者的收支平衡点。通过总结盈亏平衡点的变化,可以清楚地发现在某些情况下,攻击者为攻击付出的代价很小,攻击可以为攻击者带来丰厚的利润。
0x02 Probability of Successful Attack
在本节中将针对提出的攻击模型研究成功攻击的可能性。使用下表中所示的一些参数来开发数学公式,这些公式的灵感来自中本聪的白皮书,Grunspan的著作[1]和Rosenfeld[2]的概率模型。
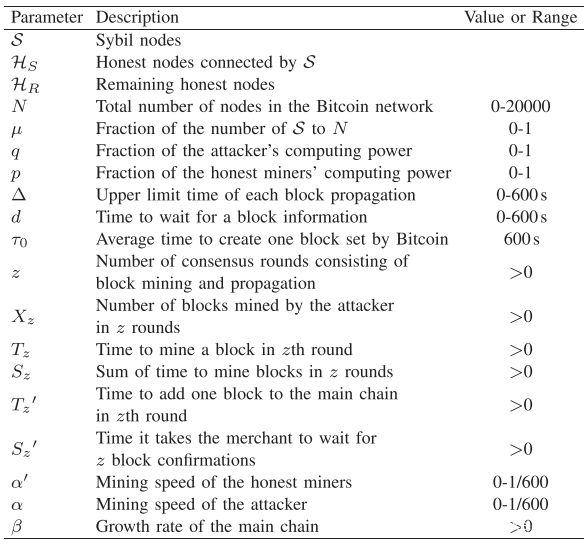
首先考虑以下两种情况,攻击者会成功进行双花。一种是攻击者以采矿速度α开采大于或等于S’z内诚实矿工开采的z区块的区块。在这种情况下,攻击者追上了主链。另一种情况是,攻击者在S’z内挖掘了k个区块,并且他也有机会以概率Pz-k赶上差距z-k。通过总结这两种情况,可以获得拟议的攻击成功的概率P:
在这里应该注意的是攻击者想要追求的目标。根据PoW中最长的链原理,无论网络中有多少链分叉,主链都是最长的链。换句话说,主链是具有最大累积计算能力的链。现在需要找出攻击者在S’z内创建k个块的概率Pr[Xz = k]。攻击者的挖掘过程与不使用Sybil攻击的情况不同。在块传播延迟的影响下,将一个块添加到主链所花费的时间T’z肯定会增加。类似地,β必定会减小。先前假设Sybil节点尝试在每个共识轮次中延迟块传播,以使d超过Δ。因此,在每个共识轮中,将一个区块添加到主链的实际花费时间为:Tz +Δ。这样就可以得到T’z的期望值:
其中α’与诚实矿工的计算能力有关,而α与攻击者的计算能力有关。如前所述,一个矿工的计算能力在总计算能力中所占的比例等于其在整个网络中总采矿速度的比例。然后有:
回想一下,除Sybil节点以外的所有节点都将参与块挖掘。因此,网络中的总挖掘速度等于攻击者和诚实矿工的挖掘速度之和。有:
通过结合(3)和(4),可以得到:
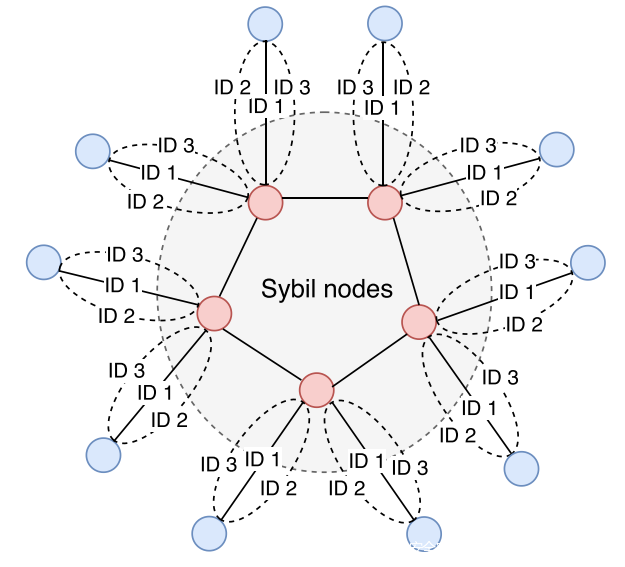
但是,由于存在区块链分叉,一些诚实节点的计算能力将被浪费。实际上E[Tz]不等于1 /α’,并且用于计算主链中PoW的哈希率会更慢。现在需要找到有效有助于主链的计算能力。根据下图所示的Sybil节点的部署,每个S连接到两个诚实节点。需要考虑两种情况:
1)新区块由HR开采:理想情况下,最多可能有2μN个诚实节点不会在共识回合中接收到块信息(有时HS不可避免地会接收HR发送的块信息,因此实际数目小于2μN),它们将开始下一个在分叉链上进行采矿和采矿。如果HR具有更大的计算能力,那么将浪费大约2μN诚实节点的计算能力。
2)新块由HS开采:在这种情况下,HR可能不会在共识回合中收到区块信息,他们将在分叉链中进行挖掘。但是,如果HR具有更大的计算能力,则分叉链将成为主链,将浪费近2μN的诚实节点的计算能力。
结合以上两种情况可以推断出,如果HR的计算能力大于或等于HS,则其计算能力被浪费的诚实节点数最多为2μN。在概率2的诚实节点的计算能力被浪费并且HR的计算能力大于或等于HS的假设下,对概率P进行以下计算。接下来,根据这个结论可以获得计算能力被浪费的节点与所有诚实节点的比率δ。它遵循:
因为每个诚实节点都具有相同的计算能力,所以可以在p中获得浪费的部分pwaste和有效部分p ∗:
接下来修改(2),然后使用(5)和(7)获得E[Tz]和E[T’z]的表达式。它遵循:
显然,一个矿工的平均采矿时间和他的平均采矿速度是彼此的倒数。因此可以使用(9)中的E[T’z]表示增长率β。它遵循:
函数Pr[Xz = k]不是泊松分布,挖掘一个块所花费的时间是无记忆的,并且总的挖掘时间具有伽马分布,因此泊松分布系数中的时间变量t是具有伽马分布而不是期望值的随机变量。根据概率公式,分布函数可以表示为:
接下来,使用伽玛分布和伽玛函数的某些属性来简化(11),首先假设:
然后将(11)简化为:
如上所示,在提出的攻击模型中攻击者的挖掘过程也是负二项式分布。已经知道概率Pr[Xz = k],计算Sybil攻击成功双花的概率的最后一步是确定攻击者追上主链的概率(即Pz-k),即他开采了k个块的情况。中本聪曾经研究过这个问题。他认为这个问题类似于赌徒的废墟问题,可以通过使用马尔可夫链的属性来解决,但是在这里需要修改中本聪的公式。在假设情况下,攻击者的挖矿速度不再与诚实矿工的挖矿速度相比,而是主链的增长率。因此,诚实矿工的采矿速度α’也被β所替代。它遵循:
公式(5),(10),(12)和(13)可用于对(1)进行简化。因此,最终公式为:
其中:
设置Δ= 100 s来计算(14)以获得拟议攻击模型的P。将P与在中本聪的攻击模型中成功进行双花的概率(即在没有任何攻击的帮助下进行双花的攻击)进行比较。使用(14)并修改λ1和λ2的值,因为中本聪的攻击模型没有链叉和块传播延迟。
上图(a)给出了比较结果,可以清楚地看到当q = 0.25时具有不同比率μ的结果。通常,随着块数z的增加,概率P降低。但是可以看到Sybil攻击的效果。与没有Sybil攻击的情况(即中本聪模型)相比,概率P得到了显着提高。即使在z等于10的情况下,当μ= 16%时P也会超过20%,而当μ= 20%时P也会接近50%。此外,很明显地发现,Sybil节点的数量越多,攻击成功的可能性就越大。请注意,μ= 20%的情况是攻击的理论最佳效果。当μ= 20%时,HS具有与HR相同的计算能力。因此,可能存在两条具有相同长度的叉状链。攻击者想要追上的目标始终是最长的链。当μ增加时,攻击者追求的目标成为HS创建的叉状链。在这种情况下,将降低Sybil攻击的影响,这解释了为什么在假设μ≤20%的情况下执行P的计算。
图(b)描绘了当z = 6(比特币设置的安全块数)时,在攻击者不同的计算能力下P随着μ的增加而变化。还显示了可以彻底破坏比特币区块链的攻击者计算能力q的最小值,可以发现q≥0.32的攻击者在最多部署20%N个Sybil节点时具有100%成功攻击的可能性,其中q = 0.32是销毁比特币的阈值区块链。换句话说,拥有32%的计算能力足以成功重写区块链历史,这远低于中本聪提出的q = 50%和Decker [3]提出的q = 49.1%。因此,结合以上分析得出结论,Sybil攻击可以大大提高双花攻击的效果。
0x03 Economic Evaluation
在本节中通过计算攻击者的收益和损失对攻击模型进行收支平衡分析。通过这种经济分析,还提供了一种从挖掘博弈双方的角度评估攻击模型的方法:对于攻击者,他们如何才能在提议的攻击中最大程度地获利?对于诚实的矿工,他们如何减少攻击者的攻击欲望?
通过以下假设简化此复杂的经济问题:
1)攻击者想要获得的商品的价值为v,假设此价值对于商家和攻击者都是相同的。
2)众所周知,如果双花攻击成功,攻击者将获得商品价值而无需支付v。此外,如果攻击失败,攻击者仍将获得v,而他必须将v支付给商家以购买这种商品。
3)此外,攻击者还将在自己的分支上支付开采区块的费用。假设攻击者挖掘一个区块的成本等于每个区块的奖励。挖掘区块的成本是每个区块的奖励与区块数量的乘积。因此,在赢得竞争的情况下攻击者将发布自己的区块,并获得自己的全部区块奖励,从而抵消了采矿成本。相反,如果攻击者失败,则他所开采的所有区块将被拒绝,他将失去这些区块的全部奖励。
在k<z的情况下,很难估算成功完成攻击后花费的时间和攻击者开采的区块数,所以确定了经济评估的范围是攻击者的收支平衡点在S’z时间内,商家等待z确认。现在开始计算攻击者的费用,用O表示攻击者在商人等待z确认之时所开采的区块数量的期望值。令r表示每个区块奖励。如果攻击者失败(概率为1-P),他将损失S’z内的总值v + Or。因此,他在S’z内的攻击代价为:
无论攻击者成功与否,他的奖励总是v,很容易得出攻击者的利润公式:
可以使用前面提到的一些已知变量来表示O。O等于每单位时间开采的块数的期望值乘以S’z的预期值(每单位时间开采的块数和S’ z是独立随机变量)。每单位时间开采的区块数量的预期值实际上是攻击者的平均开采速度α。因此剩下的问题是S’z的期望值的计算。已经从(9)知道了T’z的期望值,因此E [S’z]等于诚实矿工在S’z倍数E [T’z]中开采的区块数。它遵循:
接下来,可以通过使用(18)来简化(16):
其中r设置为12.5BTC,τ0设置为600s。攻击者的收支平衡点是一种情况,即他的成本等于其收入,因此将π设置为0。然后可以得到攻击者的收支平衡点的表达式:
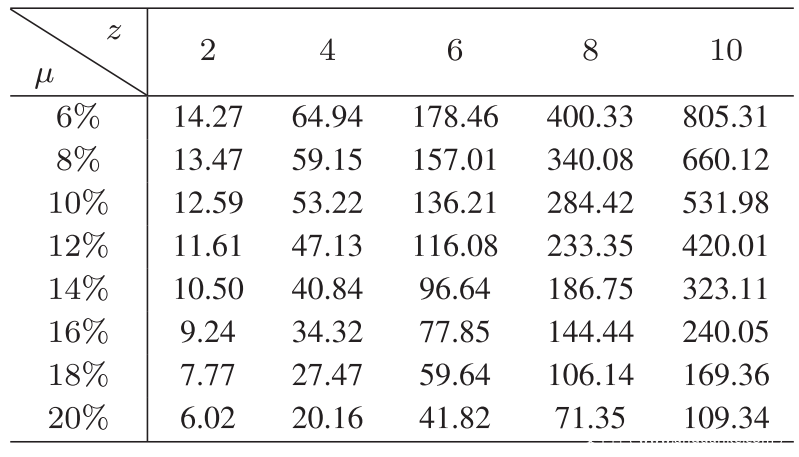
通过计算(20)可以得出攻击者在q = 0.25时随着μ和z的增加而达到的盈亏平衡点。设置变量的范围,以使块数z从2到10,步长为2,并且Sybil节点的比率μ从6到20%,步长为0.02,收支平衡点的不同结果显示在下表中。
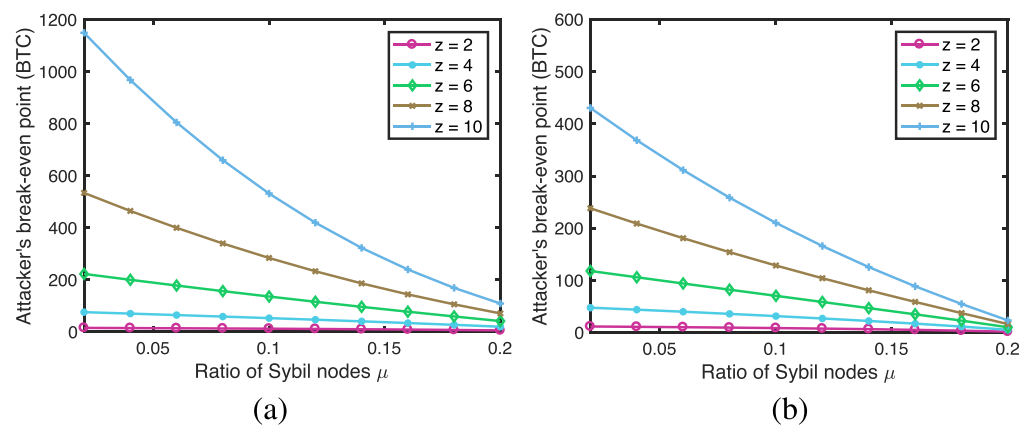
从表中可以轻松地发现,在Sybil节点μ的任何比率下,盈亏平衡点都随着z的增长而急剧增加。下图(a)和(b)在q = 0.25和q = 0.3的情况下更直观地表明了这一变化。显然,商家花费在等待确认上的时间越长,成功攻击的可能性就越低。此外,下图还说明了在任何z下,盈亏平衡点随着μ和q的增长而稳定下降。通常,与不使用Sybil攻击的情况相比,攻击者通过部署多个Sybil节点更容易获利。
为了从攻击中获利,攻击者需要确保其收入大于收支平衡点。因此,当他的收支平衡点低时,从进攻中受益很容易。在计算成功攻击概率的讨论中,已经了解到概率P将随着μ的增长而增加。这意味着如果攻击者以较高的概率P成功进行了攻击,则他将有更大的机会来抵消其挖掘成本。因此如果P高,则攻击者的收支平衡点将非常低,这对他有利。总之在Sybil攻击的影响下,双花攻击的成功概率不仅增加,而且攻击者也有很大机会获得丰厚的利润。根据所示的结果可以知道,诚实的矿工可以延长等待的区块确认数量,也可以增加商品价值,由于攻击者的高成本和低利润,迫使攻击者放弃攻击。
0x04 Conclution
在本文中提出了一种组合攻击模型,该模型使用Sybil攻击来提高比特币网络中双花成功的可能性。一名攻击者可以创建许多具有多个伪身份的Sybil节点,以延迟有效块的传播,从而帮助他在与诚实矿工的挖矿竞争中占主导地位。同时在Sybil节点的影响下,将发生区块链分叉,从而浪费了一些诚实节点的计算能力。
发现在任何情况下,提出的攻击成功的可能性都比中本聪的攻击模型大得多,并且比特币网络中32%的计算能力份额足以使攻击者重写区块链历史。此外,还从经济学的角度分析了攻击。结果表明,提出的攻击还可以使攻击者轻松获利。建议是必须提高已确认块数和商品价值,以防止攻击者的恶意行为。
Reference
[1] C. Grunspan et al., “Double spend races,” J.Enterprising Culture (JEC),vol. 21, no. 08, pp. 1–32, 2018.
[2] M. Rosenfeld, “Analysis of hashrate-based double spending,” Preprint,2014, arXiv:1402.2009.
[3] C. Decker and R. Wattenhofer, “Information propagation in the bitcoin network,” in Proc. IEEE P2P, IEEE, 2013, pp. 1–10.