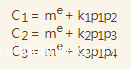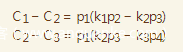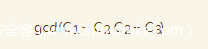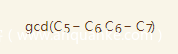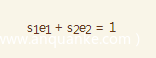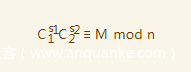Crypto-RSA多等式攻击小结

360安全客 安全知识 118971 4

前言

最近遇到一些RSA题目，里面不乏一些多等式的题目，在这里小结一下

 

多等式之公约数（1）

题目如下

m = xxxxxxxx
e = 65537
========== n c ==========
n = 20474918894051778533305262345601880928088284471121823754049725354072477155873778848055073843345820697886641086842612486541250183965966001591342031562953561793332341641334302847996108417466360688139866505179689516589305636902137210185624650854906780037204412206309949199080005576922775773722438863762117750429327585792093447423980002401200613302943834212820909269713876683465817369158585822294675056978970612202885426436071950214538262921077409076160417436699836138801162621314845608796870206834704116707763169847387223307828908570944984416973019427529790029089766264949078038669523465243837675263858062854739083634207
c = 974463908243330865728978769213595400782053398596897741316275722596415018912929508637393850919224969271766388710025195039896961956062895570062146947736340342927974992616678893372744261954172873490878805483241196345881721164078651156067119957816422768524442025688079462656755605982104174001635345874022133045402344010045961111720151990412034477755851802769069309069018738541854130183692204758761427121279982002993939745343695671900015296790637464880337375511536424796890996526681200633086841036320395847725935744757993013352804650575068136129295591306569213300156333650910795946800820067494143364885842896291126137320

n = 20918819960648891349438263046954902210959146407860980742165930253781318759285692492511475263234242002509419079545644051755251311392635763412553499744506421566074721268822337321637265942226790343839856182100575539845358877493718334237585821263388181126545189723429262149630651289446553402190531135520836104217160268349688525168375213462570213612845898989694324269410202496871688649978370284661017399056903931840656757330859626183773396574056413017367606446540199973155630466239453637232936904063706551160650295031273385619470740593510267285957905801566362502262757750629162937373721291789527659531499435235261620309759
c = 
.........

因为太多，我就不给全了，一共20组，每组一个c一个n
这是典型的多模数题目，即用同样的公钥加密同样的消息，只是私钥一直在变换
所以这就是一个简单的RSA共享素数攻击，在生成p和q的时候，难免会有2个n共享1个素数
所以我们用gcd遍历n，相应的脚本如下，即可分解出p和q

# -*- coding:utf-8 -*-
import libnum
import gmpy2
import primefac
f = open('rsa.txt','rb')
txt_content = f.readlines()[3:]
n=[]
c=[]
e=65537
for i in txt_content:
    if 'n' in i:
        n.append(int(i[4:].replace('n','')))
    elif 'c' in i:
        c.append(int(i[4:].replace('n','')))

for i in range(0,19):
    for j in range(i+1,20):
        if primefac.gcd(n[i],n[j]) != 1:
            now_n = n[i]
            now_c = c[i]
            p = primefac.gcd(n[i],n[j])
            q = now_n/p
            phi = (p-1)*(q-1)
            d = gmpy2.invert(e,phi)
            print libnum.n2s(pow(now_c,d,now_n))

即可得到flag

 

多等式之公约数（2）

题目如下

#! /usr/bin/python2.7
from Crypto.Util.number import size,bytes_to_long,getStrongPrime
from itertools import combinations

msg = bytes_to_long("Your secret flag is : flag{**************************}")
e = 65537
pri = []

f = open('cipherx.txt', 'w')

for i in range(5):
    pri.append(getStrongPrime(1024,65537))
for k in combinations(pri, 2):
    n = k[0] * k[1]
    print k[0],k[1]
    f.write(str(pow(msg, e, n)) + 'n')

题目的意思很清楚，即生成5个强素数
然后两两组合，生成10组不同的n
然后分别加密同一个消息，用同一个公钥
于是可以有下面的方程组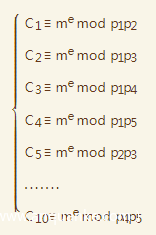这样的情况，我们显然需要数学推导
我们单独拿出下面3个式子做推导

可以推导出

其中k1,k2,k3为整数
我们式1，2相减，式2，3相减，得到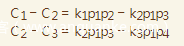
我们进行因式分解，可以得到

于是乎，我们可以进行

这样得到的公约数极大可能为p1，若不是，再做后续简单分解即可
而这道题里，公约数即为p1
所以同理，我们利用

同样可以求出p2
即

至此我们分解出了p1和p2
这即为第一组的p和q，利用其即可求出私钥解密得到消息
脚本如下

import primefac
import gmpy2
import libnum
c1 = ......
c2 = ......
c3 = ......
c5 = ......
c6 = ......
c7 = ......
e = 65537
k1 = primefac.gcd(abs(c1-c2),abs(c2-c3))
k2 = primefac.gcd(abs(c5-c6),abs(c6-c7))
n = k1*k2
phi = (k1-1)*(k2-1)
d = gmpy2.invert(e,phi)
print libnum.n2s(pow(c1,d,n))

 

多等式之共模攻击

这个方法应该大家都耳熟能详了，原理大致如下：
我们有条件即利用

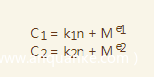
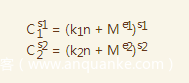
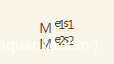
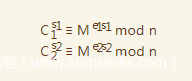
我们可以将式子1，2写成如下形式然后式子1两边同时进行s1次方，式子2进行s2次方，得到
右边的高次展开式中，除了最后一项
一定每一项都含有n，所以同时取余n的时候，只剩下最后一项
上下两式相乘，即可得到
又因为

所以可以得到

那么就很容易写出相应的脚本了

n = ......
c1 = ......
c2 = ......
e1 = 13604999
e2 = 12165379
s1,s2,tmp = libnum.xgcd(e1,e2)
if s1 < 0:
    s1 = - s1
    c1 = gmpy2.invert(c1, n)
elif s2 < 0:
    s2 = - s2
    c2 = gmpy2.invert(c2, n)
m = pow(c1, s1, n) * pow(c2, s2, n) % n
print libnum.n2s(m)

 

多等式之低加密指数广播攻击

这其实是前面公约数的变形，因为e是低指数，所以可以使用中国剩余定理，题目也很容易，即用相同的公钥加密相同的消息，但每一组的n不同，e是一个很小的数，例如3或者10
所以我们有条件:（这里以e=10为例）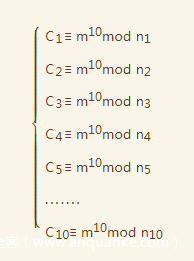
那我们看一下什么是中国剩余定理：
用现代数学的语言来说明的话，中国剩余定理给出了下列式子的一元线性同余方程组有解的判定条件，并用构造法给出了在有解情况下解的具体形式：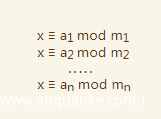
即，利用上述关系，我们可以求出x
但是有条件，即需要
这里显然满足，因为这里如果不互素，我们显然可以利用gcd分解出p或q，即文章的第一种情况
根据中国剩余定理，可以有通解
其中
所以根据这则定理，我们可以写出如下脚本

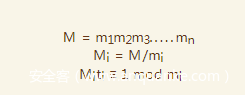
import gmpy2
import gmpy
import libnum

question = [c1,c2,c3....n1,n2,n3...]
N = 1
e=10
for i in range(len(question)):
    N*=question[i]['n']
N_list = []
for i in range(len(question)):
    N_list.append(N/question[i]['n'])
t_list = []
for i in range(len(question)):
    t_list.append(int(gmpy2.invert(N_list[i],question[i]['n'])))
sum = 0
for i in range(len(question)):
    sum = (sum+question[i]['c']*t_list[i]*N_list[i])%N
sum = gmpy.root(sum,e)[0]
print libnum.n2s(sum)
（完）