前言
LFSR(线性反馈移位寄存器)已经成为如今CTF中密码学方向题目的一个常见考点了,在今年上半年的一些国内赛和国际赛上,也出现了非常多的这类题目,但是其中绝大多数题目目前都没有writeups(或者writeups并没有做cryptanalysis,而是通过爆破的方法解决,这种思路只适用于部分类似去年强网杯出现的几道非常基础的LFSR类题目有效,对于绝大多数国际赛上的题目不仅是没有任何效果的,也是没有任何意义的,只有真正掌握了LFSR的密码学原理,才有可能在国际赛上解决一道高分值的LFSR类题目),网上针对这类考点的详细分析也不多,因此接下来我将通过几篇文章,对这类知识点进行一个详细的分析。
LFSR简介
在介绍LFSR之前,我们先对它的归属有一个大致的了解,LFSR是属于FSR(反馈移位寄存器)的一种,除了LFSR之外,还包括NFSR(非线性反馈移位寄存器)。
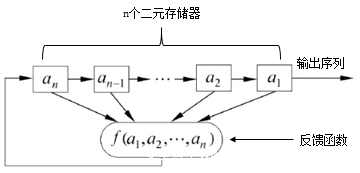
FSR是流密码产生密钥流的一个重要组成部分,在GF(2)上的一个n级FSR通常由n个二元存储器和一个反馈函数组成,如下图所示:
如果这里的反馈函数是线性的,我们则将其称为LFSR,此时该反馈函数可以表示为:
其中ci=0或1,⊕表示异或(模二加)。
我们接下来通过一个例子来更直观的明确LFSR的概念,假设给定一个5级的LFSR,其初始状态(即a1到a5这5个二元存储器的值)为:
其反馈函数为:
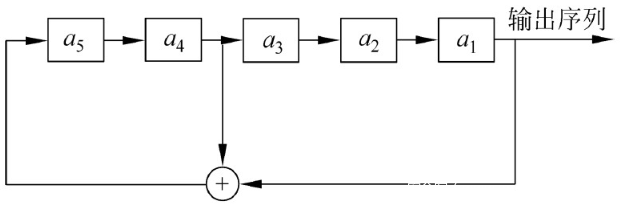
整个过程可以表示为下图所示的形式:
接下来我们来计算该LFSR的输出序列,输出序列的前5位即为我们的初始状态10011,第6位的计算过程如下:
第7位的计算过程如下:
由此类推,可以得到前31位的计算结果如下:
1001101001000010101110110001111
对于一个n级的LFSR来讲,其最大周期为2^n-1,因此对于我们上面的5级LFSR来讲,其最大周期为2^5-1=31,再后面的输出序列即为前31位的循环。
通过上面的例子我们可以看到,对于一个LFSR来讲,我们目前主要关心三个部分:初始状态、反馈函数和输出序列,那么对于CTF中考察LFSR的题目来讲也是如此,大多数情况下,我们在CTF中的考察方式都可以概括为:给出反馈函数和输出序列,要求我们反推出初始状态,初始状态即为我们需要提交的flag,另外大多数情况下,初始状态的长度我们也是已知的。
显然,这个反推并不是一个容易的过程,尤其当反馈函数十分复杂的时候,接下来我们就通过一些比赛当中出现过的具体的CTF题目,来看一下在比赛当中我们应该如何解决这类问题,由于不同题目之间难度差异会很大,所以我们先从最简单的题目开始,我将尽可能的用最通俗的语言和脚本来进行演示,在后面会逐渐提升题目的难度,同时补充相应的代数知识。
CTF例题演示
2018 CISCN 线上赛 oldstreamgame
题目给出的脚本如下:
flag = "flag{xxxxxxxxxxxxxxxx}"
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==14
def lfsr(R,mask):
output = (R << 1) & 0xffffffff
i=(R&mask)&0xffffffff
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1
output^=lastbit
return (output,lastbit)
R=int(flag[5:-1],16)
mask = 0b10100100000010000000100010010100
f=open("key","w")
for i in range(100):
tmp=0
for j in range(8):
(R,out)=lfsr(R,mask)
tmp=(tmp << 1)^out
f.write(chr(tmp))
f.close()
分析一下我们的已知条件:
已知初始状态的长度为4个十六进制数,即32位,初始状态的值即我们要去求的flag。
已知反馈函数,只不过这里的反馈函数是代码的形式,我们需要提取出它的数学表达式。
已知输出序列。
那么我们的任务很明确,就是通过分析lfsr函数,整理成数学表达式的形式求解即可,接下来我们一行一行的来分析这个函数:
#接收两个参数,R是32位的初始状态(即flag),mask是32位的掩码,由于mask已知,所以我们就直接把他当做一个常数即可。
def lfsr(R,mask):
#把R左移一位后低32位(即抹去R的最高位,然后在R的最低位补0)的值赋给output变量。
output = (R << 1) & 0xffffffff
#把传入的R和mask做按位与运算,运算结果取低32位,将该值赋给i变量。
i=(R&mask)&0xffffffff
#从i的最低位向i的最高位依次做异或运算,将运算结果赋给lastbit变量。
lastbit=0
while i!=0:
lastbit^=(i&1)
i=i>>1
#将output变量的最后一位设置成lastbit变量的值。
output^=lastbit
#返回output变量和lastbit变量的值,output即经过一轮lfsr之后的新序列,lastbit即经过一轮lfsr之后输出的一位。
return (output,lastbit)
通过上面的分析,我们可以看出在这道题的情境下,lfsr函数本质上就是一个输入R输出lastbit的函数,虽然我们现在已经清楚了R是如何经过一系列运算得到lastbit的,但是我们前面的反馈函数都是数学表达式的形式,我们能否将上述过程整理成一个表达式的形式呢?这就需要我们再进一步进行分析:
mask只有第3、5、8、12、20、27、30、32这几位为1,其余位均为0。
mask与R做按位与运算得到i,当且仅当R的第3、5、8、12、20、27、30、32这几位中也出现1时,i中才可能出现1,否则i中将全为0。
lastbit是由i的最低位向i的最高位依次做异或运算得到的,在这个过程中,所有为0的位我们可以忽略不计(因为0异或任何数等于任何数本身,不影响最后运算结果),因此lastbit的值仅取决于i中有多少个1:当i中有奇数个1时,lastbit等于1;当i中有偶数个1时,lastbit等于0。
当R的第3、5、8、12、20、27、30、32这几位依次异或结果为1时,即R中有奇数个1,因此将导致i中有奇数个1;当R的第3、5、8、12、20、27、30、32这几位依次异或结果为0时,即R中有偶数个1,因此将导致i中有偶数个1。
因此我们可以建立出联系:lastbit等于R的第3、5、8、12、20、27、30、32这几位依次异或的结果。
将其写成数学表示式的形式,即为:
显然,lastbit和R之间满足线性关系,那么接下来我们就可以开始求解了:
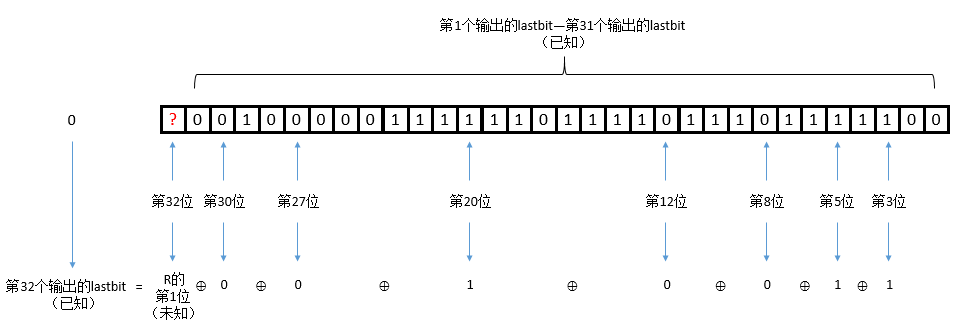
我们想象这样一个场景,当即将输出第32位lastbit时,此时R已经左移了31位,根据上面的数学表达式,我们有:
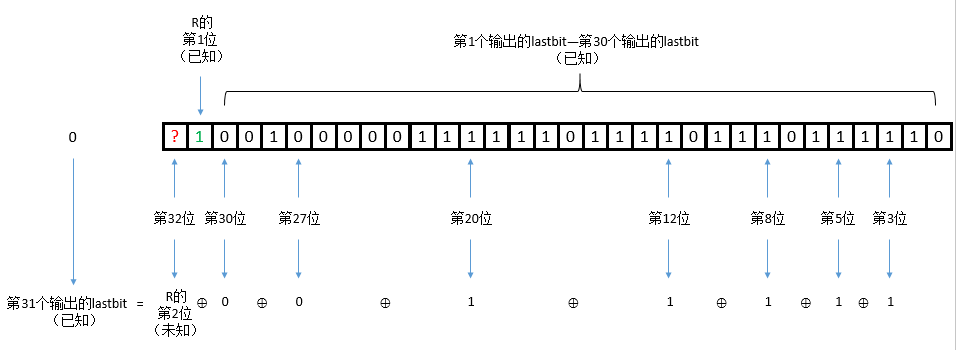
这样我们就可以求出R的第1位,同样的方法,我们可以求出R的第2位:
以此类推,R的全部32位我们都可以依次求出了,将这一计算过程写成代码形式如下:
mask = '10100100000010000000100010010100'
key = '00100000111111011110111011111000'
tmp=key
R = ''
for i in range(32):
output = '?' + key[:31]
ans = int(key2[-1-i])^int(output[-3])^int(output[-5])^int(output[-8])^int(output[-12])^int(output[-20])^int(output[-27])^int(output[-30])
R += str(ans)
key = str(ans) + key[:31]
R = format(int(R[::-1],2),'x')
flag = "flag{" + R + "}"
print flag
运行代码即可得到flag:flag{926201d7}
如下题目的分析方法同上:
2018 强网杯 线上赛 streamgame1
2018 强网杯 线上赛 streamgame2
2018 强网杯 线上赛 streamgame4
2018 HITB-XCTF 线上赛 streamgamex
总结
在本篇文章中,我们首先对CTF中LFSR类题目的基本模型做了一个介绍,然后通过一道比较典型的CTF题目,对如何在比赛中解决这类题目做了进一步的阐述。诚然,这只是LFSR类型题目的冰山一角,在后面的文章中,我们会逐渐提示LFSR题目的难度,同时补充上对应的代数知识,感谢大家的阅读。
参考
https://ctf-wiki.github.io/ctf-wiki/crypto/streamcipher/fsr/intro/